von Werner Sticht
Ein Blick in die Astronomie
Dieser Text ist eine Ergänzung zum Artikel
Wo kommt alles her?".
Nur was in dem Artikel gebraucht wird, wird hier näher erklärt. Wer mehr wissen
will, sei auf die Literaturangaben hingewiesen.
Ich kann hier den Internetauftritt
Abenteuer Universum von Halim Paracki nur
empfehlen, wo man weit mehr Einzelheiten zur Astronomie findet.
Es ist mir im Folgenden nicht wichtig, die neuesten Methoden zu beschreiben.
Es ist historisch viel interessanter, wie Menschen zu dem beschriebenen Wissen
kamen, wie sie das Wissen anwendeten und verbesserten.
Dadurch erhalten wir Beispiele, wie man durch eigenes Denken zu neuem Wissen
gelangen kann. Wir lernen, Wege zum Wissen zu finden.
Inhalt
Objekte der Astronomie
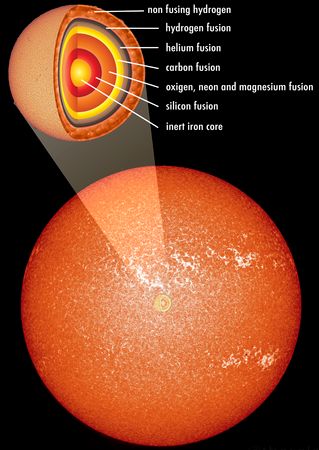
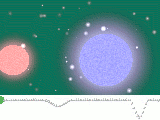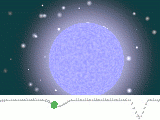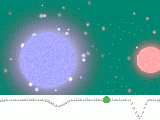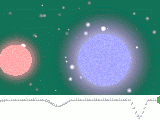
Das folgende Bild zeigt in den Teilbildern 1 und 2
Planeten
unseres Sonnensystems. Sie sind klein gegenüber den anderen Objekten.
Die anderen Objekte sind Sterne, die am Himmel selbst leuchten.
In ihrem Innern läuft eine Kernfusion ab.
Wenn ein Objekt unter 13 Jupitermassen liegt, zählt es zu den planetaren
Objekten.
Klicken Sie auf das Bild und Sie kommen zum
Original in der Wikipedia.
Wenn Sie dort mit der Maus ein Objekt des Bildes berühren, so erscheinen
Links, mit denen Sie sich zur Objektbeschreibung gelangen können.
Wenn Sie dort nur das Bild, also kein Objekt, zweimal anklicken,
bekommen Sie eine Vergrößerung.
Wie misst man Entfernungen im Weltall?
(Zu dem Thema hat auch Dieter Ortner einen Artikel geschrieben:
Distanzbestimmung.)
Der Radius der Erde
Das Verfahren stammt aus der Zeit um 200vuZ und geht auf Eratosthenes von
Kyrene zurück.
Wenn in Syene, heute Assuan (im Bild S) die Sonne senkrecht in einen Brunnen
scheint, so trifft sie in Alexandria (im Bild A) unter einem Winkel
φ auf.
φ = 7,2 Grad oder 1/50 von 360°.
Die Entfernung von Alexandria nach Syene (im Bild δ) ist 835km.
Hieraus ergab sich als Erdumfang das 50fache der Entfernung von Alexandria nach
Assuan, also 41.750 km. Eratosthenes lag 4,2 Prozent über dem heutigen Wert
(r=6371km, U=40030km).
Radius des Mondes und sein Abstand zur Erde
Aristarchos von Samos fand wahrscheinlich als erster ein
Verfahren, die Größe des Mondes zu bestimmen und auch dessen Abstand von der
Erde.
Aristarchos lebte etwa zwischen 310 vuZ und 230 vuZ. Er vertrat die Ansicht,
dass die Erde sich um die Sonne dreht, und dass die Sonne im Mittelpunkt des
Weltalls stehe.
Leider sind Aristarchos Werke verloren gegangen. Einige seiner Angaben sind
auch falsch. So nahm er an, der Mond erscheine am Himmel unter einem Winkel von
2°. Aber Aristarchos Gedanken wurden von anderen Autoren überliefert.
In den folgenden Erklärungen habe ich die richtigen Werte - anstelle der Werte
des Aristarchos - eingearbeitet.
Aristarchos Ideen entstanden aus seinen Beobachtungen bei einer totalen
Mondfinsternis.
Er maß die Zeit, während der der Mond den Kernschatten der Erde durchquerte.
Das ist jene Zeit, in der der Mond nur dunkel und blutrot leuchtet.
Das Verhältnis dieser Zeit zur gesamten Umlaufzeit lieferte ihm nun den Winkel
(in Bild unten δ=1,38°), den der Kernschatten auf der Mondbahn
einnimmt.
Da der Mond von der Erde aus unter einem Winkel von etwa 0,52° erscheint, passt
der Mond damit 2,65-mal in den Kernschatten.
Das Bild unten dient ausschließlich zur Erklärung der weiteren
Überlegungen. Es ist nicht maßstäblich.
S ist der Mittelpunkt der Sonne, E der der Erde und M der des Mondes.
SS' ist der Radius der Sonne, EE' der der Erde. MM' ist jedoch der Radius des
Kernschattens der Erde.
SE ist der Erdbahnradius. EM ist der Mondbahnradius.
Aufgrund der Winkelsumme von Dreiecken erkennt man:
α + β = γ + δ oder auch
EE'/ES' + EE'/EM' = SS'/ES + MM'/EM'.
Weil ES' fast 400-mal größer ist als EM', darf man EE'/ES' wegfallen lassen.
Eine Unterscheidung zwischen sin und tan erübrigt sich bei solch kleinen
Winkeln ebenfalls. Es bleibt: EE'/EM' = SS'/ES + MM'/EM'
Die Griechen wussten damals schon, dass die Sonne am Himmel unter dem gleichen
Winkel erscheint wie der Mond. Ganz deutlich erkennt man das bei einer
Sonnenfinsternis, bei der der Mond exakt die Sonnenscheibe
abdeckt.
SS'/ES ist die Hälfte des Winkels (γ=0,26°), unter dem uns die Sonne am
Himmel erscheint. Wir dürfen also diesen Bruch durch RM/EM ersetzen.
RM ist dabei der Radius des Mondes. Es bleibt: EE'/EM' = RM/EM + MM'/EM'
Da in den Radius MM' des Kernschattens der Mondradius 2,65-mal hinein passt,
ergibt sich nun aus der obigen Formel
EE'/EM' = RM/EM + 2,65 ⋅ RM/EM' oder, weil EM = EM', auch
EE' = 3,65 ⋅ RM oder RM = EE' / 3,65.
EE' hat bereits Eratosthenes gefunden. Also gilt: Der Mondradius RM ist
1747km (6378km/3,65).
Somit findet man: Die Entfernung Erde-Mond EM ist 385071km
(weil RM/EM=0,26°/360°⋅2π=9,0757E-3)
Aristarchos fand seinerzeit heraus, dass der Abstand Erde-Mond 60 Erdradien
betrage. Er erhielt somit EM=382680km. Heute weiß man, dass EM zwischen 356400km
(geringstes Perigäum) und 406700km (größtes Apogäum)
schwankt.
Heute misst man den Abstand Erde-Mond allerdings mit Laserpulsen. Man schickt
einen Puls zu einem Spiegel auf dem Mond und wartet, bis das Licht nach etwa
2,6 Sekunden wieder zurückkommt. Diese Zeit kann man sehr genau messen.
Daraus kann man auch den Abstand Erde-Mond sehr genau bestimmen.
Dass der Kernschatten der Erde kreisförmig ist, dient zusätzlich noch als ein
Nachweis der Kugelgestalt der Erde.
Fortschritte am Anfang der Neuzeit
Nach Aristarchos gab es noch viele Fortschritte in der Astronomie, etwa durch
Hipparchos oder durch
Claudius Ptolemäus, der mit einem Buch das gesamte Wissen
seiner Zeit - auch mit Sternkarten - veröffentlichte. Das Werk war die
Grundlage allen astronomischen Wissens bis in die Neuzeit. Es ist unter dem
arabischen Namen Almagest bekannt, und es ist ein Gesamtwerk der Astronomie,
aber auch der zugehörigen Mathematik.
Die Sterndaten des Almagest gehen bis zu einer Auflösung von etwa
20 Bogenminuten. Der Kreisumgang wird in 360 Grad (°) unterteilt.
Jedes Grad wird dann noch in je 60 Bogenminuten (') geteilt.
Eine Bogenminute wird weiter in je 60 Bogensekunden (") eingeteilt.
Wenn man den Erdäquator als Kreis ansieht, dann ist 1° davon 111km, 1' dann
1855m (oder etwa 1 britische Seemeile), und 1" dann 30,9m.
Mit Beginn der Neuzeit wurde das antike Wissen durch den Buchdruck
in Europa verbreitet.
Nikolaus Kopernikus (1473-1543) fand wieder, dass
die Sonne der Mittelpunkt der Welt sein sollte. Er ordnete die Planeten auf
Kreisbahnen an, wobei die Sonne nicht unbedingt im Zentrum des Kreises lag.
Wie Aristarchos schon früher, musste Kopernikus erklären, warum die Sterne dann
keine Kreise am Firmament beschrieben. Aristarchos hatte die Sterne schon als
extrem weit entfernt angegeben, so dass deren Kreise so klein seien, dass man
sie nicht sehen könne.
Außerdem müssten die Sterne - wegen der großen Entfernung - dann auch
außerordentlich hohe Leuchtkräfte haben.
Mit dem Gedanken, dass es sich bei den Sternen um weit entfernte Sonnen
handelt, konnte sich damals aber kaum jemand anfreunden.
Zu den ganz großen Astronomen der Neuzeit gehören
Tycho Brahe (1546-1601) und
Johannes Kepler (1571-1630).
Brahe gelang es, die Bewegung der Planeten bis auf 2' zu vermessen - also
10-mal genauer als alle anderen vor ihm. Dabei arbeitete er noch ohne
Fernrohr.
Kurz vor seinem Tod hatte er den jungen Johannes Kepler als Assistenten.
Kepler veröffentlichte nach Brahes Tod dessen gesamte Messungen unter Brahes
Namen.
Kepler selbst untersuchte Brahes Daten. Er fand so die
Keplerschen Gesetze.
- Anhand der Daten zum Mars, fand er heraus, dass die Planeten nicht auf
exzentrischen Kreisbahnen, sondern auf Ellipsenbahnen die Sonne umlaufen, wobei
die Sonne in einem der Brennpunkte (im Bild F1) liegt.
- Der Strahl von der Sonne zum Planeten überstreicht in gleichen Zeiten
gleiche Flächen. Im Bild sind das die Flächen A1 und A2.
In der Nähe der Sonne sind die Planeten schneller.
- Bei zwei Planeten gilt :
( a1 / a2 ) 3 = ( T1 / T2 ) 2
Dabei ist a1 die große Halbachse des Planeten 1 und T1 die Umlaufzeit des
Planeten 1 um die Sonne. Die große Halbachse a1 beginnt bei F1 und geht über
F2 hinaus bis zum Rand der Ellipse.
Entsprechendes gilt für a2 und T2 für den Planeten 2.
Kleine Halbachsen bedeuten also kurze Umlaufzeiten.
Man konnte damals die Umlaufzeiten der Planeten schon genau messen. Aber
über die Abstände zur Sonne hatte man nur Verhältniszahlen.
Man wusste nur, dass der Jupiter 5,2-mal so weit von der Sonne weg ist, wie die
Erde. Man wusste aber nicht, wie viele Kilometer das sind.
Edmond Halley (1656-1742) schlug schließlich vor, den
Abstand Erde-Sonne anhand eines
Venusdurchgangs zu bestimmen.
Ein Venusdurchgang kommt in 243 Jahren nur 4-mal auf. Der Grund liegt in den
unterschiedlichen Bahnneigungen von Erde und Venus.
Weil die Venus auf der Sonnenscheibe nur einen Winkel von 1' (1/30 des
Sonnendurchmessers) ausmacht, brauchte man ein Teleskop als optische
Hilfsmittel.
Brahe, der noch ohne Fernrohr arbeitete, hätte das kaum messen können.
Das nebenstehende Bild zeigt, wie man den Venusdurchgang beobachtete.
Eine Beobachtungsstation lag auf Tahiti im Pazifik. Die andere in Vardø, im
nördlichsten Norwegen, wo der Durchgang bei Mitternachtssonne gemessen
wurde.
Man konnte mit diesen Messwerten auch gleich noch den Durchmesser von Sonne und
Venus erfassen. Mit Keplers 3. Gesetz konnte man nun alle Maße des
Sonnensystems berechnen.
Im Jahr 1666 hatte Isaak Newton (1642-1726) die glorreiche Idee, dass sich
Massen gegenseitig anziehen. Der Apfel, der vom Baum fällt, zieht auch
die Erde an. Die Erde ist wegen ihrer großen Masse jedoch träge und kann sich
dem Apfel kaum nähern.
Aufbauend auf Keplers 3. Gesetz konnte er nun das Gravitationsgesetz
formulieren: F = G ⋅ m1 ⋅ m2 / r2
Dabei ist F die Anziehungskraft zwischen den beiden Massen m1 und m2. r ist
der Abstand zwischen den Massen, und G ist die Gravitationskonstante, die man
damals noch nicht bestimmen konnte.
Als Henry Cavendish (1731-1810) im Jahr 1798 die
Gravitationskonstante (6,6743E-11) gemessen hatte, konnte
man nun auch die Massen der Sonne und der Planeten angeben - zumindest
wenn diese einen Mond haben.
Mit einem Fernrohr konnte man nun auch deren Durchmesser ermitteln und damit
deren Dichte ausrechnen. Auf diese Weise stellte man fest, dass die äußeren
Planeten hauptsächlich aus Gas bestehen. Der Planet Saturn hat eine so geringe
Dichte, dass er theoretisch sogar auf Wasser schwimmen könnte.
Wenn m1>>m2 ist und m2 in einer Kreisbahn um m1 läuft, kann man die
Anziehungskraft mit der Zentrifugalkraft gleichsetzen.
G ⋅ m1 ⋅ m2 / r2 = m2 ⋅ 4π2
⋅ r / T2 →
m1 = 4π2 / G ⋅ ( r3 / T 2)
Es ergibt sich Keplers 3. Gesetz.
Entfernungsmessung mit Dreieckswinkeln

Im Mittelalter brauchte man die Entfernungen, wenn man eine Stadt mit
Kanonen beschießen wollte.
Bildherkunft
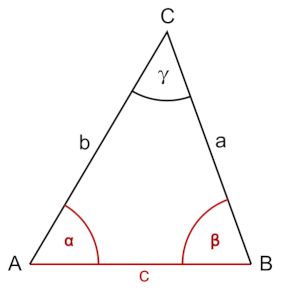
Wenn man bei einem Dreieck die Länge einer Seite und die Größe zweier Winkel
kennt, so kann man die Längen der anderen Seiten berechnen.
Es gilt
sin(α) / a = sin(β) / b = sin(γ) / c.
Wenn α=60° und β=70°, so ist γ=180°-60°-70°=50° und
sin(60°)=0,866; sin(70°)=0,94; sin(50°)=0,766.
Wenn jetzt c=20m ist, so ist a=c⋅sin(α)/sin(γ)=22,61m;
b=24,53m.
Wenn a und b sehr groß gegenüber c werden, so wird γ sehr klein.
Da sich dann α und β nicht mehr genau genug messen lassen, werden
die Längen von a und b entsprechend ungenau.
Aristarchos hat versucht, mit dieser Methode den Abstand Erde-Sonne zu messen.
An Punkt A dachte er sich den zur Hälfte bedeckten Mond - α sollte damit
90° sein. Als Strecke c nahm er den Anstand Erde-Mond.
β versuchte er zu messen: Er kam auf 87°. Damit war für ihn die Sonne
19-mal so weit weg wie der Mond.
Sein Winkel β hätte aber 89,85° sein müssen, denn die Sonne ist fast
400-mal so weit weg wie der Mond. So genau konnte er eben nicht messen.
Entfernungsmessung mit Parallaxe
Schaut man auf seinen Daumen der ausgestreckten Hand einmal mit dem linken
und dann mit dem rechten Auge, so scheint der Daumen vor dem Hintergrund hin
und her zu springen. Wenn wir weiter nur mit einem Auge auf den Daumen schauen,
jetzt aber den Kopf hin und her bewegen, so wird sich auch der Hintergrund
her und hin bewegen. Diese Verschiebungen nennt man
Parallaxe.
Wenn wir nun im Frühjahr auf den Himmel schauen, so muss ein naher Stern
an einer anderen Stelle am Himmel erscheinen als im Herbst - ein halbes Jahr
später.
Durch die jährliche Bewegung der Erde um die Sonne verschiebt sich ein naher
Stern vor dem nahezu unendlich weit entfernten Hintergrund im
Halbjahresrhythmus.
Der Stern (im Bild rot) beschreibt eine Ellipse am Firmament.
Denken wir uns den Abstand Frühjahrspunkt und Herbstpunkt der Erdbahn - also
den Erdbahndurchmesser - als die Basislinie eines Dreiecks.
Der Winkel an der Spitze des Dreiecks ist dann auch der Winkel, unter dem wir
die Ellipse am Firmament sehen. Daraus könnte man den Abstand des Sterns
berechnen.
Wenn wir nun, wie Aristarchos und Kopernikus, die Sonne als Zentrum der Welt
annehmen, so müssten wir diese Ellipsen finden. Nahe Sterne würden größere
Ellipsen am Himmel zeigen. Weit entfernte Sterne würden dagegen nur sehr kleine,
ja oft nur noch als Punkt erkennbare Ellipsen zeigen.
Wir würden einen nahen Stern hernehmen und dessen jährliche Wanderung am Himmel
vergleichen mit der nur noch durch einen Punkt erkennbaren Ellipse eines ganz
fernen Sterns.
Das Problem der Astronomen war der Winkel an der Spitze des Dreiecks - und
damit auch die Ellipse der allernächsten Sterne - beide sind außerordentlich
klein. Aristarchos und auch Brahe konnten sie noch nicht messen.
Es hat bis in die 1830er Jahre gedauert, bis
verlässliche Messwerte zu den Ellipsen vorlagen.
Selbst beim nächsten Stern
Proxima Centauri beschreibt die Ellipse am Himmel nur einen
Winkel von 0,768 Bogensekunden. Dieser Stern ist 4,24 Lichtjahre weg.
Aber fast alle Sterne sind hunderte, ja abertausende Lichtjahre weg.
Es gab in den 1830er Jahren mehrere Astronomen, die sich mit diesen Ellipsen
beschäftigt haben. Der Astronom
Bessel aus Königsberg (heute Kaliningrad) hat sein
Messverfahren derart anschaulich beschrieben, dass man von
ihm heute sagt, er habe als erster die Entfernung eines Fixsterns gemessen.
Bessel verwendete ein spezielles Fernrohr mit einer Brennweite von 2,6m und
einem Objektivdurchmesser von 158mm. Jeder Stern wird bei dieser Öffnung als
ein Beugungsscheibchen von 0,8" (" = Bogensekunde) im
Brennpunkt dargestellt.
Er arbeitete mit einer Vergrößerung von 300.
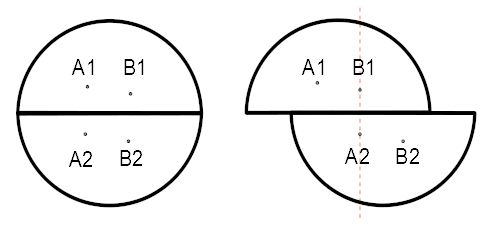 Bessels Fernrohr, ein Heliometer, hatte vorne - in Richtung zum Stern - eine
geteilte Linse. Die beiden Halblinsen konnte man sehr genau gegeneinander
verschieben. Es ergaben sich so für jeden Stern zwei Brennpunkte, jeweils durch
die obere und die untere Teillinse. Durch Verschieben der einen Teillinse
konnte man nun den einen Brennpunkt des Sterns (A2) mit dem zweiten Brennpunkt
des anderen Sterns (B1) mittels einer Mikrometerschraube übereinander bringen.
Eine Verschiebung einer Teillinse um 1mm entsprach bei Bessels Heliometer einem
Winkelunterschied von etwa 80".
An einer Skala konnte man den Winkelabstand mit einer Genauigkeit von 0,05"
ablesen.
Das Fernrohr kann zum Messen beliebig um seine Längsachse gedreht werden.
Bessels Fernrohr, ein Heliometer, hatte vorne - in Richtung zum Stern - eine
geteilte Linse. Die beiden Halblinsen konnte man sehr genau gegeneinander
verschieben. Es ergaben sich so für jeden Stern zwei Brennpunkte, jeweils durch
die obere und die untere Teillinse. Durch Verschieben der einen Teillinse
konnte man nun den einen Brennpunkt des Sterns (A2) mit dem zweiten Brennpunkt
des anderen Sterns (B1) mittels einer Mikrometerschraube übereinander bringen.
Eine Verschiebung einer Teillinse um 1mm entsprach bei Bessels Heliometer einem
Winkelunterschied von etwa 80".
An einer Skala konnte man den Winkelabstand mit einer Genauigkeit von 0,05"
ablesen.
Das Fernrohr kann zum Messen beliebig um seine Längsachse gedreht werden.
Bessel wählte für seine Arbeit den Doppelstern
61 Cygni,
der fast das ganze Jahr in Königsberg beobachtet werden konnte. 61 Cygni hat
eine hohe Eigengeschwindigkeit (5,2" pro Jahr) und die beiden Teilsterne waren
damals durch einen Winkel von 16,2" getrennt. Bessel sah beides als Kriterien
für einen Stern nahe bei der Sonne.
Nun brauchte er noch zwei Vergleichssterne, die weit genug von der Sonne
entfernt waren, so dass sie keine wahrnehmbare Parallaxen zeigten.
Der eine Vergleichsstern a lag etwa senkrecht zu den Doppelsternkomponenten
in einem Winkel von etwa 462". Der andere Vergleichsstern b lag etwa auf der
Verbindungslinie in ungefähr 706" Abstand. Die Änderung dieser Winkel sollte
später die Parallaxe zeigen.
Vom März 1837 bis Oktober 1838 hat Bessel nun 85-mal den Abstand zu
Vergleichsstern a und 96-mal zu Vergleichsstern b gemessen. Er hat die
Temperatur und den Luftdruck notiert, um die Linsenwirkung der Erdatmosphäre
berücksichtigen zu können.
Die Eichung des Heliometers war zudem temperaturabhängig.
Jede seiner Abstandsmessungen wurde mit bis zu 16 verschiedenen Einstellungen
des Heliometers überprüft.
Bei der Endauswertung aller Daten wurden die jährlichen Eigenbewegungen von
61 Cygni und die der Vergleichssterne noch herausgerechnet. Nutation der Erde
und Aberration wurden berücksichtigt.
Als Ergebnis gab er einen Parallaxenwinkel von 0,3136" an und eine Entfernung
von 10,28 Lichtjahren. Heute nennt man als Entfernung 11,4 Lichtjahre.
Die Leistung Bessels kann man sich veranschaulichen, wenn man die
gemessenen Winkel betrachtet. Der Durchmesser des Mondes erscheint uns
von der Erde aus unter einem Winkel von etwa 1872". Der Abstand von 61 Cygni
zum Vergleichsstern b war etwa 700". Dieser Abstand änderte sich im Laufe
eines Halbjahres um 0,3", also um etwa 0,04% oder um etwa ein 6240-stel des
Monddurchmessers. Und diese 0,3" mussten zweifelsfrei herausgearbeitet
werden.
Man mag fragen, warum Bessel einen so hohen Aufwand getrieben hat. Dabei muss
man berücksichtigen, das es damals noch keine Fotoplatten gab, auf denen man
die Abstände der beteiligten Sterne hätte aufnehmen und später ausmessen können.
Man konnte das gesehene Bild nur abzeichnen. Aber das war nicht sehr genau.
Deshalb entstanden damals als Behelf
aufwendige Heliometer, wie eben das in Königsberg.
Gefertigt wurde es im
Mathematisch-Feinmechanische Institut in München von
Fraunhofer.
Man kann mit der Parallaxenmethode von der Erde aus nur Sternentfernungen bis
etwa 100 Lichtjahre messen. Als man später mit dem
Dopplereffekt die Eigenbewegung des Sonnensystems messen
konnte, war man auch nicht mehr durch die Erdbahn eingeschränkt. Man verglich
Fotos, die vor mehreren Jahren gemacht wurden, mit neuen Fotos.
Dann konnte man die Wegstrecke unserer Sonne in diesen Jahren als Basislinie
einer Triangulation hernehmen.
Immerhin bewegt sich das Sonnensystem in der Scheibe der Milchstraße
mit etwa 267km/s, im Jahr etwa 8,4 Milliarden km oder das 28-fache des
Erdbahndurchmessers. Bei derartigen Messungen ist jedoch auch die
Eigenbewegung der zu untersuchenden Sterne und ihrer
Nachbarn unbedingt zu berücksichtigen. Die Ungenauigkeit ist nicht gering.
Satelliten, etwa Hipparcos oder das neuere System
Gaia können mit der reinen Triangulation inzwischen viel
weiter messen. Gaia kann Entfernungen bis zu 18000 Lichtjahren mit einem Fehler
unter 20% bestimmen.
Scheinbare und absolute Helligkeit von Sternen
Die Sterne am Himmel erscheinen uns unterschiedlich hell. Das hat schon
Hipparchos in seinem Sternkatalog vermerkt. Den hellsten
Sternen ordnete er die Größe 1 zu, den gerade noch sichtbaren die Größe 6.
Als man später die Helligkeiten genauer messen konnte, war eine Festlegung
erforderlich, die der bisherigen Regelung weitgehend entsprach. Man hat für die
scheinbare Helligkeit eine logarithmische Skala geschaffen.
0mag entspricht dabei etwa der Helligkeit von Wega. Ein Stern von 5mag ist nach
Festlegung nur noch 0,01 mal so hell, wie 0mag - also um den Faktor 100 weniger.
Damit hat ein Stern von 1mag eine um den Faktor 2,512 (= 100**0.2) verkleinerte
Helligkeit als 0mag. 2mag ist dann wieder 2,512-mal weniger hell als 1mag.
Je höher der mag-Wert desto schwächer erscheint uns der Stern.
Die scheinbare Helligkeit ist in den gängigen Sternkarten vermerkt.
Beispiele: Sonne -26,78; Mond -12,5; Sirius -1,46; Wega 0,04; 61 Cyg A 5,22;
61 Cyg B 6,03 (Bessels Stern).
Ein Stern am Himmel, der uns als hell erscheint, muss nicht unbedingt ein
großer Stern sein. Es kann auch ein kleiner Stern sein, der nur nahe bei der
Sonne steht. Deshalb hat man die
absolute Helligkeit eingeführt als diejenige Helligkeit,
mit der der Stern aus einer Entfernung von 32,6 Lichtjahren oder 10 Parsec
oder unter einem Parallaxenwinkel von 0,1" erscheinen würde.
Die absolute Helligkeit der Sonne beträgt nur 4,84mag.
Die absolute Helligkeit eines Sterns kann man berechnen, wenn man die
Entfernung des Sterns kennt.
Die Formel dazu ist M = m + 5 − 5 ⋅ lg(a) oder
M = m − 5 ⋅ lg(a / 10)
Dabei ist: M absolute Helligkeit; m scheinbare Helligkeit;
lg() = log10()
a Abstand oder Entfernung in Parsec, wobei 1 Parsec = 3,26 Lichtjahre ist.
Man sollte noch den Unterschied zur
bolometrischen Helligkeit kennen. Diese Helligkeiten
beziehen sich auf das gesamte
elektromagnetische Spektrum, während sonst nur das
sichtbare Licht
berücksichtigt ist.
Es gibt die scheinbare mbol und die absolute bolometrische
Helligkeit Mbol. Die normale Helligkeit bezeichnet man zur
Unterscheidung oft mit mv - v für visuell.
Es gilt immer mbol ≤ mv. Der kleinere
bolometrische mag-Wert deutet auf eine größere Strahlungsleistung hin.
Die Sterne strahlen ja auch im Infrarot und um Ultraviolett, was in der
Atmosphäre verschluckt wird.
Man kann mbol aus dem
Planckschen Strahlungsgesetz berechnen:
mbol = mv − BC.
Dabei wird vorausgesetzt, dass der Stern auch wie ein Schwarzer Körper strahlt.
Das ist aber nur annähernd der Fall. Deshalb entnimmt man BC besser aus
Sterntabellen. BC nennt man die Bolometrische Korrektur.
Mehr Hinweise unten.
Entfernungsmessung mit Cepheiden
Nach dieser kurzen Einführung in die Sternhelligkeiten wollen wir zu den
veränderlichen Sternen kommen.
Um veränderliche Sterne zu finden, muss man einen zu untersuchenden
Himmelsausschnitt wiederholt fotografieren.
Bei einer Auswertung solcher wiederholter Aufnahmen machte die Astronomin
Henrietta Leavitt eine wegweisende Entdeckung.
Sie untersuchte Aufnahmen der großen und der kleinen
Magellanschen Wolke nach veränderlichen Sternen.
Diese Zwerggalaxien sind über 160.000 Lichtjahre weg. Alle Sterne darin sind so
weit weg, dass sie von uns aus als gleich weit entfernt angesehen werden
können.
Henrietta Leavitt fand dort mehrere
Pulsationsveränderliche, bei denen sich die Leuchtkraft -
und damit auch die absolute Helligkeit - in regelmäßigen Zeitabständen
änderte, und die Helligkeitsschwankungen sich regelmäßig wiederholten.
Dabei stellte sie auch noch fest, dass bei diesen Sternen die Wiederholungsrate
mit der mittleren Leuchtkraft zusammen hing. Je heller der Stern (niedrigerer
mag-Wert) war, desto länger die Zeit zwischen den Maxima.
Sie hat das in den Diagrammen oben festgehalten. Es sind Kurven der Maxima und
der Minima der scheinbaren Helligkeiten eingezeichnet. Der Abstand der Kurven
beträgt etwa 1,2mag. Auf der x-Achse finden wir beim linken Diagramm die
Periodendauer in Tagen angegeben. Beim rechten Diagramm ist die Periodendauer
logarithmisch dargestellt. Es ergeben sich rechts Geraden.
Wenn man nun einen dieser besonderen Sterne in der Nähe der Sonne fände, so
könnte man durch eine Parallaxenmessung dessen Entfernung bestimmen.
Dann könnte man damit dessen absolute Helligkeit berechnen.
Würde man solche Sterne dann irgendwo im Weltall finden, so könnte man aus
der Pulsationsdauer und der Helligkeit deren Entfernung bestimmen.
Man hat bald mit δ Cephei einer dieser Sterne in der Milchstraße
gefunden. Man gab den Sternen deshalb den Namen
Cepheiden.
Die Cepheiden haben Pulsationsperioden liegt zwischen 2 und 45 Tagen.
Während der Pulsation ändern sie auch ihren Durchmesser und ihre Farbe.
Leider sind die nächsten Cepheiden so weit von der Sonne entfernt,
dass man sie damals mit Parallaxen nicht messen konnte. Bei δ Cephei
sind es 887 Lichtjahre.
Aber die Cepheiden sind sehr hell - 1000 bis 10000-mal so hell wie die Sonne.
Man konnte sie deshalb sogar in den Nachbargalaxien, etwa im
Andromedanebel, auffinden.
Bereits in den 1920er Jahren versuchte man mit Erkenntnissen, die später zum
Hertzsprung-Russell-Diagramm führten, die absolute
Helligkeit der Cepheiden zu bestimmen. Das gelang zuverlässig jedoch erst
Walter Baade im Jahr 1952, als er feststellte, dass es zwei verschiedene Typen
von Cepheiden, die
klassischen Cepheiden und die
W-Virginis-Sterne, gab. Letzte hatte man zur Eichung in den
1920er Jahren fälschlicherweise genommen.
Deshalb ist in Büchern der 1920er bis 1950er Jahre die Entfernung zum
Andromedanebel zu niedrig angegeben.
Dank der Cepheiden kann man heute die Entfernung zum
Andromedanebel mit 2,5 Millionen Lichtjahren
angeben.
Vor Henrietta Leavitts Entdeckung hatte man schon herausgefunden, dass
Kugelsternhaufen mehrere zehntausend Lichtjahre entfernt sind. (Siehe
Riesen).
Mit den Cepheiden konnte man nun diese Schätzungen untermauern.
Wenn man noch größere Entfernungen im Weltall bestimmen will, kann man auf
die Rotverschiebung nach Hubble-Lemaître
zurückgreifen.
Aber das ist heute noch nicht alles. Manche Doppelsterne explodieren am Ende
in einer besonderen Supernova Typ Ia. Bei ihrer
Explosion wird eine ziemlich genau definierte Energie frei. Aus dieser Energie
kann man die Entfernung berechnen.
Was sagt uns das Licht aus dem Weltall?
Das Sehen ist der wichtigste Sinn des Menschen. Deshalb haben sich Menschen
schon lange damit auseinander gesetzt. Dabei ist von den Menschen ein Gegensatz
zwischen Licht und Finsternis erdacht worden.
Mit Licht wurde Offenheit, Güte, Sicherheit in Verbindung gebracht, während
zur Finsternis das Unheimliche, das Böse und die Gefahr gerechnet wurden.
Wenn es hell ist, sieht man eben besser. Die Finsternis - oder der Mangel an
Licht - wurde da zur Gefahr personifiziert.
Allerlei Vorstellungen sind da in der Vergangenheit entstanden, die inzwischen
auch wieder verschwunden sind, wie man im Wikipedia-Artikel zu Goethes
Farbenlehre nachlesen kann.
Es dauerte bis etwa 1670, bis sich
Isaak Newton mit dem Licht beschäftigte und zeigte, wie
weißes Licht durch ein Prisma in Farbstrahlen zerlegt wird.
Fast unser ganzes Wissen über das Weltall haben wir erhalten durch die
Elektromagnetische Strahlung, die vom Himmel zu uns
gekommen ist. Es sind zwar auch einige
Meteoriten
auf die Erde gefallen - auch sie haben unser Wissen über unser Sonnensystem
erweitert. Aber unser Wissen über Sterne und Galaxien stammt in erster Linie
aus dem Licht.
Die Elektromagnetischen Strahlung ist eine Wellenstrahlung, die man nach
Wellenlänge oder nach Frequenz in einem
Spektrum anordnen kann.
Das folgende Bild zeigt Wellenlängen an. Die Farbe ist jedoch abhängig von der
Frequenz. Wenn das Licht in Materie eintritt, die einen höheren Brechungsindex
hat, so sinken dort die Wellenlänge und die Lichtgeschwindigkeit. Aber die
Frequenz und die Farbe bleiben.
Die Strahlung, die als sichtbares Licht wahrgenommen werden kann, ist nur ein
Ausschnitt aus dem Gesamtspektrum.
Das menschliche Sehen
Man könnte nun annehmen, dass das menschliche Auge innerhalb des
sichtbaren Lichts für alle Wellenlängen gleich empfindlich sei. Das ist aber
nicht der Fall.
Auf Wellenlängen am Rand des sichtbaren Bereiches ist eine höhere
Strahlungsintensität nötig, um dieselbe Helligkeitsempfindung zu bewirken als
in seiner Mitte.
Die Helligkeitsempfindung ist bei verschiedenen Menschen unterschiedlich.
Deshalb zeigen die folgenden Diagramme statistisch verwertbare Mittelwerte über
eine ausreichend große Gruppe von Menschen.
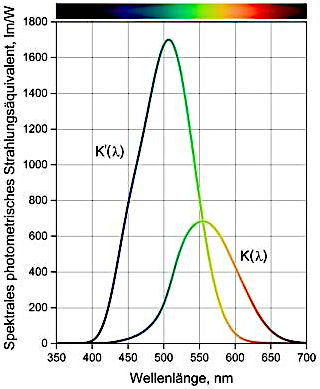
Das Bild rechts zeigt uns das
Helligkeitsempfinden des menschlichen Auges, auch
Photometrisches Strahlungsäquivalent genannt.
Je größer der Wert ist, desto größer ist der für das Auge nutzbare
Lichtstrom bei gegebener Strahlungsleistung einer Lichtquelle.
Bei Tagsehen gilt die Kurve K(λ). Das Maximum der Kurve
K(λ) liegt bei einer Wellenlänge von 555nm.
1 Watt physikalischer Strahlungsleistung wird bei dieser Wellenlänge wie ein
Lichtstrom von 683 Lumen empfunden. Bei anderen Farben wird die
Strahlungsleistung von einem Watt als dunkler eingeschätzt.
Beim Nachtsehen gilt die Kurve K'(λ). Das menschliche
Sehvermögen ist nachts deutlich empfindlicher als tags.
Dafür kann man nachts die Farben kaum unterscheiden.
Aufbauend auf dem menschlichen Sehen hat man das System der
Photometrie aufgebaut. Dort werden Einheiten wie
Lumen
(für Lichtstrom),
Candela
(für Lichtstärke - 1 Candela entspricht etwa einer Kerze) und
Lux
(für Beleuchtungsstärke) als Einheiten verwendet.
Eine Zuordnung zu den in Physik und Astronomie verwendeten Größen findet man in
dem Wikipedia-Artikel zur Radiometrie. Dort werden als entsprechende Begriffe
die Strahlungsleistung in Watt,
die Strahlungsstärke in W/sr und die
Bestrahlungsstärke (oder Strahlungsflußdichte) in
W/m2 benützt.
Diese Einheiten decken dann auch das
Infrarot, das
Ultraviolett und sogar die
Gammastrahlung ab.
Nicht nur das Helligkeitsempfinden, sondern auch das System der menschlichen
Farbwahrnehmung weicht offensichtlich vom Spektrum ab.
Wenn wir als Menschen das Spektrum des sichtbaren Lichts ansehen, so erkennen
wir, dass es doch einige Farben mehr gibt, als wir im Spektrum des sichtbaren
Lichts finden können. Im Spektrum des Lichts fehlen beispielsweise die Farben
Weiß, Schwarz, Beige, Braun, Pink, Purpur.
Die Farbe Schwarz ist dabei ein Fehlen von Licht, Weiß ist eine ganz besondere
Farbenmischung. Die Farbe Beige ein dunkles Gelb, Braun ein dunkles Orange.
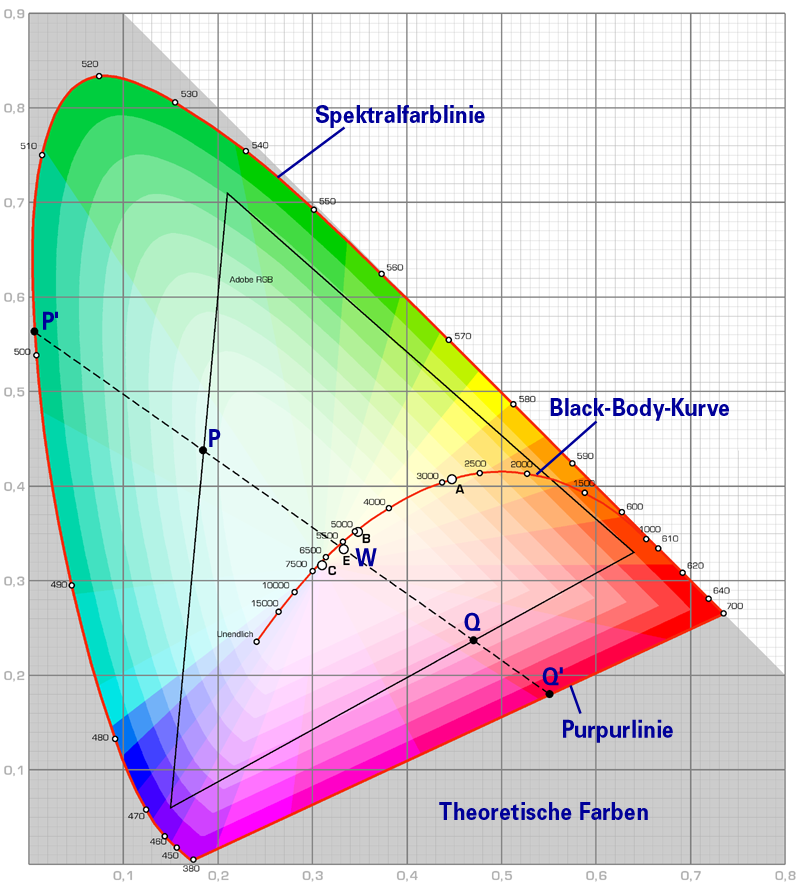
Das Bild rechts ist eine Darstellung des
CIE-Normfarbsystems, das uns die Art des
menschlichen Farbsehens verdeutlicht.
Es zeigt uns auf dem äußeren Bogen die Spektralfarben.
Die Farben der Purpurlinie kommen im Spektrum nicht vor, auch die Farbe weiß
in der Mitte nicht. Diese Farben werden von der menschlichen Farbwahrnehmung
errechnet und als Sinneseindruck an das Gehirn weiter gegeben.
Die menschliche Farbwahrnehmung ist ein ganz besonderes
Rechenprogramm.
Wenn wir im CIE-Diagramm eine rote Farbe mit einer grünen Farbe durch eine
Strecke verbinden, so finden wir in der Mitte der Strecke die Farbe Gelb.
Das menschliche Farberkennungssystem aus Auge und Hirn berechnet aus dieser
Rot-Grün-Kombination die Farbe Gelb und leitet sie als Eindruck ins Gedächtnis
weiter. Dieses so berechnete Gelb ist jedoch nicht das Gelb aus dem Spektrum,
sondern es ist ein Wahrnehmungsfehler der menschlichen Farberkennung.
Die Konstruktionsprinzip von RGB-Farbmonitoren und Displays nützt den Fehler
aus und baut darauf auf.
Ebenso können wir eine blaue Farbe mit der gelben Farbe verbinden, und wir
finden die Farbe Weiß. Auch durch Verbinden der Punkte P' und Q', oder auch
schon durch Verbinden von P und Q trifft man den Weißpunkt W.
Gerade weil das menschliche Sehen so frequenzabhängig ist, wurden Spektren
früher bevorzugt auf Film aufgenommen. Ein Film kann mehr Farben darstellen,
als ein Mensch sieht. Weiterhin ist die Empfindlichkeit über einen größeren
Frequenzbereich weitgehend gleich.
Heute verwendet man besondere Halbleiterdetektoren.
Die Sonnenstrahlung und ihr Spektrum
(Zu den Themen Strahlung und Spektren haben Björn Malte Schäfer & Markus Pössel
einen Artikel mit vielen Bildern geschrieben:
Welche Informationen liefert Strahlung?.)
Die Strahlung des Schwarzen Körpers
Fast all unser Licht kommt als
Sonnenstrahlung zu uns. Wir können uns die
Sonne als
ein extrem heißes Stück Materie vorstellen - als einen strahlenden
Schwarzen Körper. Der Schwarze Körper sendet Licht
in einem weiten zusammenhängenden Bereich von Wellenlängen aus;
entsprechend dem Planckschen
Strahlungsgesetz.
Man nennt das ein kontinuierliches Spektrum. Der Schwarze Körper strahlt
nur aufgrund seiner Temperatur. Er nimmt dabei alle von außen kommende
Strahlung auf, spiegelt aber keine.
Als Beispiel nehmen wir ein heißes Stück Eisen, das beim Schmieden ja zunächst
rötlich glühen kann. Wenn man es noch mehr erhitzt, wird es orange bis gelb
glühend.
Der Glühfaden in einer Glühbirne kann sogar etwa 4000° heiß werden.
Temperaturen bis 50000° findet man in besonderen bläulich leuchtenden Sternen.
Die Black-Body-Kurve im CIE-Diagramm oben zeigt eine Zuordnung von Temperatur
zur Farbe. Die Farbe ändert sich nur leicht, wenn die Temperatur steigt.
Die starke UV-Strahlung bei hohen Temperaturen wird vom Auge nicht
wahrgenommen.
Das Bild rechts zeigt mit der oberen Kurve und gelbem Hintergrund, auf
welchen Wellenlängen ein Schwarzer Körper von 5900° der Theorie nach
strahlt.
5900° ist etwa die Temperatur der Sonnenoberfläche. Wir sehen, dass der
Höchststand der Strahlung bei einer Wellenlänge von etwa 500nm liegt.
Aber auch in nicht mehr sichtbaren
Ultraviolett (UV) und im
Infrarot (IR) strahlt die Sonne.
Vom UV bekommen wir Sonnenbrand. IR nehmen wir als Wärmestrahlung wahr.
Die außerhalb der Atmosphäre der Erde in Wirklichkeit ankommende
effektive Strahlung zeigt im Bild die Kurve mit dem
orangenen Hintergrund. Die Sonne ist eben nur annähernd ein Schwarzer
Körper. Die Abweichung kann aus dem Spektrum (siehe unten)
ermittelt werden.
Diese Strahlung muss dann noch durch die Atmosphäre.
Was unten auf der Erde ankommt, zeigt die unterste schwarze Kurve
mit dem Farbspektrum. Wir erkennen, dass da viel Licht durch die Lufthülle
ausgefiltert wurde.
Wir erkennen, dass der harte gefährliche UV-Strahlung fehlt. Sie wird großteils
durch die Ozonschicht herausgefiltert.
Aber auch bei der Infrarotstrahlung gibt es große Lücken, die die Moleküle der
Luft - insbesondere der
Wasserdampf - verursacht haben. Die Moleküle haben
dieses Licht aufgenommen und als Wärme gespeichert.
Diskrete Strahler
Außer der Strahlung des Schwarzen Körpers gibt es auch andere
Lichtquellen, die kein kontinuierliches Spektrum aussenden.
Ein Beispiel ist eine normale Flamme eines Feuers. Darin findet man Teile eines
kontinuierlichen Spektrums, aber auch auffällige intensive
Spektrallinien.
Bei Gasentladungslampen, etwa
Energiesparlampen oder
Neonröhren, findet man kaum mehr Anteile
des kontinuierlichen Spektrums.
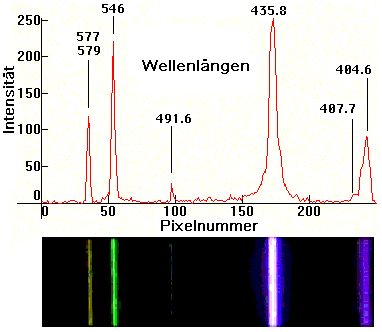
Sie liefern ein diskretes Spektrum - ein
Linienspektrum. Siehe Bild rechts.
Wenn man einem Gas Energie zuführt, so können dessen Atome die Energie als Licht
nur in festgelegten Portionen wieder abgeben. Man nennt diese Portionen
Photonen.
Die wichtigste Eigenschaft des Photons ist seine Energie und damit seine
Frequenz und Farbe.
(E = h ⋅ f oder E = h ⋅ c / λ ).
Man gibt die Farbe oft auch als Wellenlänge λ in Nanometern an.
Es stehen dem Atom jedoch mehrere verschiedene Energieportionen zur
Verfügung, über die es Licht abstrahlen kann. Man fasst sie als
Emissionsspektrum zusammen. Im Bild rechts erkennt
man vier Farblinien aus diesem Spektrum.
Ein Gas kann also nur Licht in einer bestimmten Farbkombination abstrahlen.
Und diese Farbkombination ist typisch für das Gas. Man kann das Gas
aufgrund der Farbkombination identifizieren, also eindeutig bestimmen.
Und wenn man ein Gas nun mit Photonen bestrahlt, so erkennt man, dass es
genau die Photonen auch aufnehmen kann, welche es bei Energieüberschuss
aussendet. Andere Photonen kann es nicht aufnehmen.
Fraunhofer-Linien
Wenn man in einem Spektrum den Bereich des sichtbaren Sonnenlichtes
vergrößert, so sieht man dort Einschnitte. Es gibt viel mehr davon, als das
folgende Bild darstellt. Mit diesen Einschnitten wollen wir uns nun
näher beschäftigen.
Es sind die Fraunhofer-Linien.
Joseph Fraunhofer hat sie zwar nicht als erster entdeckt,
er hat sie aber 1814 als erster genau vermessen und beschrieben.
Er hat selbst über 570 davon gefunden. Es gibt aber unzählige mehr.
Diese schwarzen Linien im Bild oben müssen auf dem Weg
von der Sonnenoberfläche bis zur Erdoberfläche entstanden sein.
Irgendein Vorgang muss da Licht aus dem Spektrum herausgenommen oder
"absorbiert" haben. Deshalb heißt ein solches Spektrum auch
Absorptionsspektrum.
Ein Absorptionsspektrum entsteht, wenn Licht eines kontinuierlichen Spektrums
ein Gas durchstrahlt.
Genau so, wie ein Gas nur bestimmte Photonen (oder Energieportionen) aussenden
kann, so kann es auch nur gleichartige Photonen aufnehmen oder
absorbieren.
Dabei schluckt das Gas die Photonen und strahlt sie gleichförmig verteilt
in alle Raumrichtungen wieder ab.
Man findet diese Photonen deshalb im hindurch tretenden Licht nicht mehr.
Die Photonen wurden absorbiert, und das Spektrum des hindurch tretenden Lichts
ist bei den betreffenden Wellenlängen dunkel oder sogar schwarz.
Das Absorptionsspektrum charakterisiert diese Materie, die von
der Strahlung durchquert wird.
| Linie | Stoff | λ |
| A | O2 | 759,370 |
| B | O2 | 686,370 |
| C | H α | 759,719 |
| D1 | Na | 589,594 |
| D2 | Na | 588,997 |
| D3 | He | 587,562 |
| F | H β | 486,134 |
| G | Fe | 430,790 |
| H | Ca+ | 393,847 |
Der Physiker Gustav Kirchhoff und der Chemiker
Robert Bunsen haben 1859 als erste nun Dämpfe oder Gase
verschiedenster Materialien bestrahlt, um festzustellen, welche Wellenlängen
von ihnen absorbiert werden. Durch diese beiden Herren ist die
Spektroskopie eine
wichtige Methode zur Analyse von Stoffen geworden.
Ihre Arbeiten haben gezeigt, dass die Fraunhofer-Linien den Atomen oder
Molekülen bestimmter Stoffe zuzuordnen sind. Siehe Tabelle rechts, sie
zeigt wenige Beispiele.
Die Spalte Linie nennt Fraunhofers ursprüngliche Bezeichnung. Man findet sie
auch im Bild oben.
λ nennt die zugehörige Wellenlänge in Nanometern.
- Linien A und B werden durch das Sauerstoffmolekül
O2 in der Lufthülle der Erde erzeugt.
- Linien C und F, also H α und H β
sind (Balmer-)Linien des Wasserstoffatoms, das so nur in der Sonnenatmosphäre
vorkommen.
- Linien D1 und D2 sind Linien des Natriums Na. Diese
beiden Linien sind auffällig beim Element Natrium. An diesen Linien hat man die
Absorption erstmals erkannt.
- Linie G kommt von gasförmigem Eisen Fe, was nur auf der Sonne
so vorkommt
- Linie H stammt von Calcium-Ionen Ca+, die so
auch nur von der Sonne stammen.
- Linie D3 konnte man lange nicht zuordnen. Man meinte im Jahr 1868,
ein neues Element Helium He entdeckt zu haben, das es nur auf der Sonne
gibt.
(Der Name Helium kommt von griechischen Sonnengott Helios, nicht von der
germanischen Göttin der Unterwelt namens Hel.)
Anmerkung: Zur Breite und Tiefe (sie geht nicht unbedingt bis auf die
Intensität 0 hinab) der Fraunhofer-Linien verweise ich auf andere Quellen.
Die verschiedenen Arten der
Linienverbreiterung lassen Schlüsse zu auf die Temperatur
und den Druck der beteiligten Gase.
Messungen der Wellenlänge
(Das folgende Thema hat Bernhard Grotz in einem Artikel über
Wellenoptik auch recht nett erklärt.)
Wenn wir die Wellenlängen des Lichts der Spektrallinien messen
wollen, so müssen wir etwas in die Theorie einsteigen.
Christian Huygens veröffentlichte 1678 seine
Wellentheorie des Lichts.
Nach seinen Überlegungen breitet sich das Licht als
Wellenfront aus.
Jeder Punkten einer Wellenfront ist Beginn einer
Elementarwelle.
Die Elementarwellen breiten sich kugelförmig aus. Durch gegenseitige
Überlagerung bilden sie eine neue Wellenfront.
Im Bild rechts kommt eine Wellenfront von oben. Im Spalt sind zur
Verdeutlichung gelbe Punkte gezeichnet, von denen sich nun Elementarwellen
kreisförmig nach rechts, links und weiter nach unten ausbreiten.
So entsteht daraus die neue (grüne) Wellenfront.
Das Bild zeigt, dass sich Licht also auch um die Ecke herum ausbreiten kann.
Man sagt denn, das Licht wird
gebeugt.
Das ist aber nicht der bevorzugte Weg des Lichts.
Das obere Bild zeigt die Wellenausbreitung der Elementarwellen. Sie beginnen
in den gelben Punkten mit einem Höchstwerte der Schwingung. Die grauen Linien
sind dann die Höchstwerte der folgenden Schwingungen. Die Höchstwerte der
Schwingungen wandern dann gemeinsam nach außen. Man sagt, Sie sind in
Phase.
Das Bild rechts zeigt uns im linken Teilbild, wie sich zwei Schwingungen
verstärken. Oben ist die Summe der beiden unteren Wellen.
Das rechte Teilbild zeigt uns dagegen, dass sich zwei Schwingungen auch
völlig auslöschen können. Dazu müssen die beiden Teilschwingungen nur
um 180° oder um π verschoben sein.
Wenn jedoch zwei Schwingungen um 360°, also um 2π oder um eine
oder mehrere ganze Wellenlängen verschoben sind, so verstärken sie sich,
wie im linken Teilbild.
Thomas Young hat im Jahr 1802 nun mit seinem
Doppelspalt-Experiment gezeigt, wie man die Wellenlänge
von Licht messen kann. Siehe Bild rechts.
Von links kommt eine Wellenfront, die auf eine Platte trifft, die in den
Punkten A und B einen sehr kleinen Spalt hat. Der Spalt geht in die Tiefe der
Zeichnung.
Von A und von B bilden sich nun kreisförmig Elementarwellen aus. Sie treffen
in Punkt P auf einen Schirm. Die Welle von Punkt A nach P und die Welle
von Punkt B nach P haben einen Wegunterschied BC. Wenn BC ein Vielfaches der
Wellenlänge ist, so sehen wir auf dem Schirm im Punkt P einen hellen Fleck.
Wir haben dann eine verstärkende
Interferenz.
Helligkeit, wenn BP − AP = BC = m ⋅ λ, also
bei m = 0, 1, 2, ..., aber auch bei m = -1, -2, ... . (λ steht für die
Wellenlänge.)
Das Bild zeigt den Fall, wenn m=1 ist. Es gilt auch: AP = CP.
Auslöschung erfolgt, wenn BP − AP = (m−1)/2 ⋅
λ,
bei den schon genannten Werten von m.
An Punkt M haben wir natürlich auch einen hellen Fleck. Es ist der Fall m=0.
Dort trifft die geradeaus durchlaufende Wellenfront auf.
Der Abstand der Punkte A und B ist g; er sollte nicht größer als 0,1mm sein.
Die Breite der Spalten ist b; sie sollte nicht größer als 0,05mm sein.
Den Winkel α für den ersten Helligkeitspunkt P bei m=1 kann man dann für
alle Wellenlängen berechnen durch
| λ | α |
d |
|---|
| 400nm (violett) | 0,23° oder 13,75' | 4mm |
| 500nm (grün) | 0,29° oder 17,19' | 5mm |
| 700nm (rot) | 0,40° oder 24,06' | 7mm |
sin(α) = λ / g
Wenn g = 0,1mm ist, ergeben sich die Winkel in der Tabelle rechts.
Wenn wir für den Abstand vom Doppelspalt zum Schirm noch a = 1m nehmen, so
können wir auch den Abstand MP=d berechnen.
Dabei können wir α ≈ α' setzen und weil α so klein ist,
dürfen wir auch tan(α') ≈ sin(α) setzen.
Es gilt dann: d = a ⋅ λ / g oder
λ = d ⋅ g / a
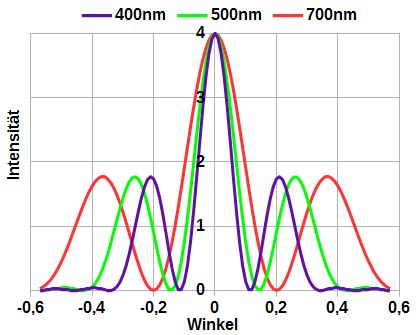 |
| Helligkeitsverteilung hinter dem
Doppelspalt. |
Das Bild rechts zeigt uns die Intensität der Strahlung auf dem Schirm.
Die X-Achse zeigt den Winkel α. Die Winkel sind recht klein.
Man wird das Bild mit einer Lupe betrachten.
Wenn ein Lichtstrahl von roter Farbe (λ=700nm) von links auf den
Doppelspalt trifft, so sehen wir in der Mitte bei Punkt M einen Lichtfleck,
der bei 0,2° völlig verschwunden oder dunkel ist. Dann steigt die Helligkeit
wieder an und hat bei 0,37° ein Nebenmaximum.
Ein grüner Lichtstrahl (λ=500nm) erzeugt schmalere Kurven. Das
erste Minimum liegt bei 0,14° und das Nebenmaximum bei 0,26°.
Beim violetten Lichtstrahl (λ=400nm) liegt das Minimum bei 0,11°
und das Nebenmaximum bei 0,21°.
Wenn nun ein weißer Lichtstrahl von links kommt, so wird in Punkt M ein
verwaschener weißer Fleck erscheinen. Daneben, von unter 0,2° bis etwa 0,5°
erkennt man verwaschen die Regenbogenfarben, innen violett, außen rot.
Wir erkennen aus dem Diagramm, dass keine genaue Messung der Wellenlänge mit
dem Doppelspalt möglich ist. Man kann lediglich die Größenordnung erkennen.
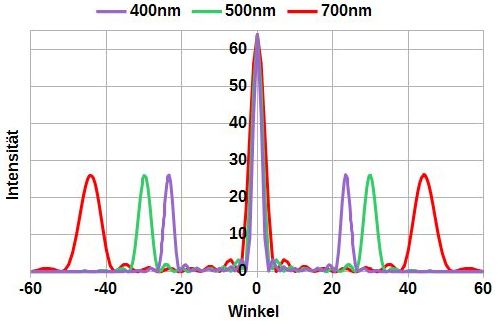 |
| Helligkeitsverteilung hinter einem Gitter mit 8
Spalten. |
Als Verbesserung hat man nun - statt nur zwei Spalten - mehrere Spalten
nebeneinander angeordnet. Man bekommt so ein
optisches Gitter.
Beim Bild rechts wurden 8 Spalten (N=8) verwendet. Abweichend zum
Doppelspalt wurde nun der Abstand zwischen den Spalten auf 1µm verringert.
Die Breite der Spalten ist nur noch 0,5µm.
Man erreicht dadurch:
- Der Winkel α ist nun bis 50° groß. Grund ist der niedrige
Spaltabstand bei 1000 Spalten pro mm. Nebenmaxima mit |m|>=2 kommen nicht
mehr vor.
- Die Intensitäten sind wegen der vielen Spalte höher. Sie steigen mit
N2.
- Die Kurven um die Nebenmaxima sind schmaler. Die Farben sind jetzt deutlich
voneinander getrennt. Die Kurven werden um so schmaler, je mehr Spalten im
Gitter sind.
- Die Nebenmaxima sind umso höher gegenüber dem Maximum in der Mitte, je
kleiner |b/g| ist. Kleinere Spaltenbreite bedeutet höhere Intensität der
Nebenmaxima.
Die Intensitäten in den Diagrammen wurden berechnet nach der
Formel für den Mehrfachspalt.
Übliche Gitter haben heute Abstände von etwa 1200 Spalten pro mm.
Sie haben Ausdehnungen über mehrere Dezimeter. Die Auflösung eines
Gitters für das m-te Nebenmaximum beträgt
λ / Δλ = m ⋅ N.
Ein Gitter mit 12000 Spalten (etwa 1dm breit) kann für m=1 also noch
Wellenlängen von 500,000nm und von 500,004nm trennen.
Übrigens: Bereits Fraunhofer hat schon optische Gitter mit 300
Spalten pro Millimeter maschinell aus Draht hergestellt.
Was bereits um 1850 technisch möglich war, zeigt der Wikipedia-Artikel über
Friedrich Adolph Nobert und seiner
Teilmaschine. Er konnte Gitter mit Spaltabständen von
0,11µm herstellen.
Spektrographen können Gitter mit Schlitzen im Metall
enthalten. Aber auch Glas, in das etwa 1000 Linien pro mm mit einem Diamant
hinein geritzt wurden, sind üblich. Es werden auch Reflexionsgitter, etwa das
Blazegitter, gerne eingesetzt.
Selbst die Spuren einer CD (Abstand = 1,6µm) können als
Spektroskop hergenommen werden. Eine
Bauanleitung und eine schöne
Erklärung findet man im Netz.
Kohärenz
Für unsere Messungen der Wellenlängen trifft eine Wellenfront von Licht
auf einen Doppelspalt oder auf ein Gitter. Wir haben bisher einfach
vorausgesetzt, dass die Wellenfront an Punkt A und Punkt B oder an all den
angestrahlten Gitterspalten die gleiche
Phase
hat. Nulldurchgang, Maximum und Minimum der Welle müssen dabei an Punkt A und
an Punkt B zur gleichen Zeit da sein.
Wenn an Punkt A und Punkt B (oder beim Gitter an den äußersten Spalten) während
unserer Beobachtung ein andauernder gleicher Phasenunterschied
wäre, so hätte das keine große Auswirkung. Wenn wir die Platte mit den Spalten
etwas drehen, so haben wir doch auch so einen dauernden Phasenunterschied und
alle Intensitäten sind nur um einen kleinen Winkel verschoben.
Wenn jedoch - innerhalb unserer Messung - sich die Phase immer wieder um
λ/2 oder um 180° ändert, so wird auf dem Schirm das Maximum und das
Minimum immer wieder gegeneinander verschoben. Die Interferenz verschwindet
dann. Wir sehen kein Spektrum mehr.
Wenn sich die Phase innerhalb der Messung um weniger als 180° ändert,
so sieht man die Interferenz noch, aber abgeschwächt. Sie verliert dann an
Kontrast.
Den höchsten Kontrast haben wir, wenn der Phasenunterschied über die Zeit der
Messung konstant bleibt. Solches Licht nennt man
kohärent.
 |
| Blendeneinstellung um Interferenz zu
bekommen. |
Wie verhindert man nun, dass sich zwischen Punkt A und Punkt B ein
Phasenunterschied von λ/2 überhaupt ausbilden kann?
Das Licht kommt aus der Blendenöffnung. Zeitlich und räumlich statistisch
verteilt - kann an jedem Punkt zwischen R und S eine Elementarwelle starten.
Wenn die Elementarwelle an Punkt M" startet, so sind die Wege M"A und M"B gleich.
Es gibt keinen Phasenunterschied an Punkt A und Punkt B.
Wenn die Elementarwelle aber in R startet, so ist der Weg RA ein kürzerer als
der Weg RB. Dann gibt es einen Phasenunterschied. Die kugelförmigen
Elementarwellen von R oder von S erzeugen die größten Phasenunterschiede.
Diese müssen kleiner als λ/2 gehalten werden, damit wir die
Interferenz sehen können. Die Blende hilft uns dazu.
Anhand vom Bild rechts wird nun gezeigt, welche Einstellungen örtlich
vor dem Doppelspalt gemacht werden müssen, damit wir rechts vom
Doppelspalt überhaupt etwas sehen.
Im Bild ist g der Abstand der Spalten beim Doppelspalt, oder es ist die volle
Breite eines Gitters mit all seinen N Spalten.
D ist der Abstand zwischen Gitter und Blende.
h ist die Blendenöffnung. Für die Strecken gilt: RM" = M"S = h/2;
AM' = M'B = g/2; RA = AT = SB; RB = SA
Die Strecke ST = SA − TA ≈ h ⋅ sin(β) ≈
h ⋅ g / 2 / D.
Weil ST < λ / 2 sein muss - damit überhaupt Interferenz auftritt - gilt
h ⋅ g / 2 / D < λ / 2 oder
g / λ < D / h oder h < D ⋅ λ / g.
(Siehe auch
Demtröder Band 2, S.287f.)
Wenn also, wie beim Doppelspalt oben, g = 0,1mm, λ = 400nm und
D = 1m, so muss die Blende h < 4mm sein.
Wenn ein Gitter mit 10000 Spalten und einer Gesamtbreite von g = 1dm
bei λ = 400nm und bei einem Abstand der Lichtquelle von 1m
(D = 1m) vom Gitter noch funktionieren soll, so ist die Blende
h < 4µm zu wählen. Wenn wir eine größere Blende nehmen, wird
das Spektrum ungenauer, verwaschener. Man hätte dann mit weniger Spalten gleich
gute Ergebnisse.
Wenn man vom Stern Alpha Centauri A ein Spektrum aufnehmen will, so
ist h = 1,7E9 m (Durchmesser des Sterns), D = 41E15 m
(Entfernung 4,34 LJ), λ wieder 400nm einzusetzen.
Damit darf das Gitter des Spektrographen höchstens 9m (g < 9,6m)
breit sein. Bei Fixsternen - nicht bei der Sonne - ist somit die
Kohärenzbedingung wohl immer erfüllt.
Die Spektren von Sternen
Sobald die Astronomen von den Möglichkeiten der Spektralanalyse erfuhren,
wurden gleich massenweise Fotos von Spektren angefertigt und in eigens dafür
geschaffenen Bibliotheken gesammelt. Am Anfang wusste man noch nicht, was da
an neuen Erkenntnissen zu erwarten wäre. Aber schon der Gedanke, etwas über die
chemische Zusammensetzung der Sterne in Erfahrung bringen zu können, war
eine gigantische Herausforderung. Aber es war nicht allein die Chemie, sondern
vor allem die Physik, die die neuen Erkenntnisse brachte.
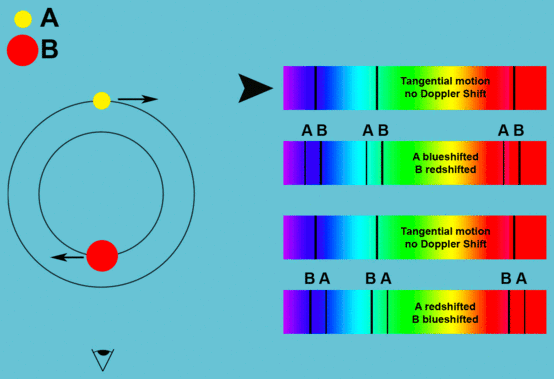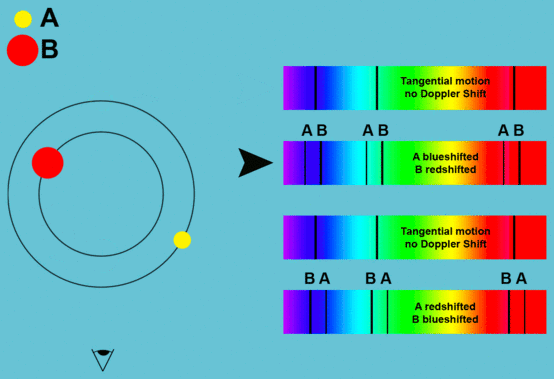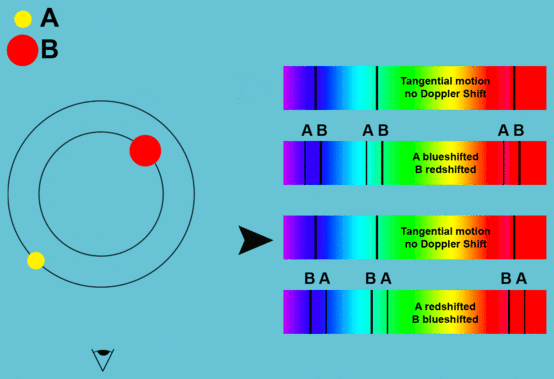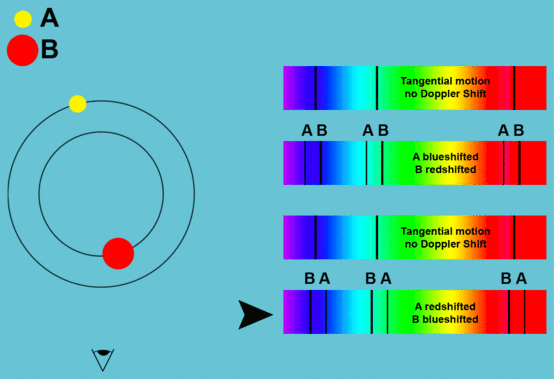
Der Doppler-Effekt
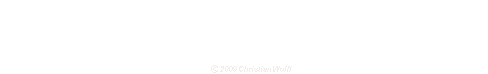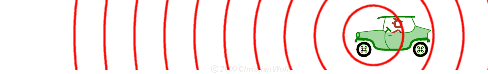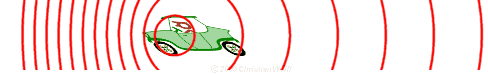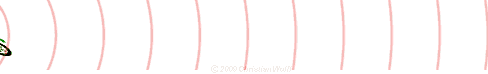 |
Änderung der Wellenlänge bei Bewegung der
Schallquelle. Bildherkunft |
Wenn der Notarzt angefahren kommt mit lautem Lalü, so ist die Tonhöhe
auffallend hoch. Wenn er aber an uns vorbeigefahren ist, ist die Tonhöhe
deutlich tiefer.
Wenn eine Schallquelle sich uns nähert, so klingt sie höher,
als wenn sie sich von uns wegbewegt. Dabei hat der ausgesendete Ton seine
Tonhöhe überhaupt nicht geändert.
Es handelt sich um den Doppler-Effekt.
Die Erscheinungen des Doppler-Effektes findet man auch in Sternenspektren.
Wenn ein Objekt sich von uns entfernt, so erscheint es nach Rot verschoben.
Wenn das Objekt sich auf uns zu bewegt, erscheint es uns nach Blau
verschoben.
Δλ / λ0 =
(λbeobachtet − λ0) /
λ0 =
λbeobachtet / λ0 − 1 =
v / c = z
Dabei ist λ0 die Wellenlänge des Strahlers, wenn er sich nicht
bewegen würde. v ist die Geschwindigkeit, mit der er sich von uns weg
bewegt. Wenn der Strahler auf uns zukommt, ist v negativ.
c ist die Lichtgeschwindigkeit. Die Formel gilt, wenn |v| sehr klein gegen c
ist. z bezeichnet man auch als
Rotverschiebung.
(Weitere Formeln bei Wikipedia.)
Die Erde kreist um die Sonne: 2 ⋅ π ⋅ 150e6 km / (365,25 ⋅
24 ⋅ 3600 s) =
29,8 km/s
Dazu kommt noch die Erddrehung: 2 ⋅ π ⋅ 6371 km /
(24 ⋅ 3600 s) = 463,3 m/s.
Selbst wenn ein Stern sich gegenüber der Sonne überhaupt nicht bewegt, so sieht
ihn ein Astronom, der auf dem Äquator steht, mit bis zu 30,25km/s auf sich
zukommen oder weg fliegen. Meist ist es etwas weniger. Man kann diese
Geschwindigkeit für jeden Punkt auf der Erde und auch für jeden einzelnen Stern
ganz genau ausrechnen.
Nach der Formel für den Doppler-Effekt müsste bei dieser Geschwindigkeit die
vom Stern gesendete Fraunhofer-Linie D1 für Na - normalerweise 589,594nm - nun
bei 589,594⋅(1-30,25/299792,458)nm = 589,535nm liegen, wenn der Stern auf
uns zufliegt. Die Abweichung beträgt nur 0,01% oder 0,06nm.
Man benötigt für Geschwindigkeitsmessungen an Sternen also sehr genau arbeitende
Spektrographen.
Der oben erwähnte Spektrograph mit 12000 Spalten könnte
beispielsweise noch Geschwindigkeiten von 2,4km/s erkennen.
Die Spektren wurden früher auf Film aufgenommen. Zusätzlich blendete man noch
die Emissionslinien einer Gasentladungsröhre mit ausgewählter Gasfüllung auf
einer getrennten Spur ins Bild mit ein. So hatte man gleich die Eichpunkte des
nicht bewegten Gases mit im Bild.
Wenn man nun die Bewegung der Sonne gegenüber einem Stern, einem
Sternhaufen oder ähnlichem Himmelsobjekt herausfinden will, so muss man in der
Regel zuerst die Bewegung der Erde gegenüber dem Objekt messen.
Ein halbes Jahr später wiederholt man die Messung. Dann ist die Erdbewegung ja
in die andere Richtung.
Der Mittelwert lieferte dann die
Radialgeschwindigkeit vr für die Bewegung
der Sonne gegenüber dem Himmelsobjekt.
Die Tangentialgeschwindigkeit des Objekts kann man erhalten, wenn man den
Eigenbewegung µ ermittelt, den der Stern im Laufe
eines oder mehrerer Jahre am Himmel zurücklegt. Man kann dabei ja auf alte
Fotos zurückgreifen. Wenn man die Entfernung r des Himmelsobjektes kennt,
errechnet man dann seine Tangentialgeschwindigkeit mit
vt = µ ⋅ r.
Aus Tangential- und Radialgeschwindigkeit ergibt sich die eigentliche
Geschwindigkeit des Himmelsobjekts.
Dass viele Sterne - auch die Sonne - auf einen Punkt im Sternbild Herkules sich
bewegten, hat bereits Wilhelm Herschel erkannt.
Argelander hat dies anhand von 390 Sternen später genau
vermessen - allein aus der Eigenbewegung.
Die Sonne bewegt sich mit 19,7km/s in Richtung des Sonnenapex. Das ist der
Ort: α = 18h00m; δ = +30°; l = 56°; b = +23°
Die Sonne führt eine Umlaufbahn mit einem
Radius von etwa 8,34 kpc (27188 Lichtjahre) im Uhrzeigersinn (aus galaktisch
Nord gesehen) um das Zentrum der Milchstraße aus. Die Bahngeschwindigkeit
beträgt etwa 255km/s und die Bahn ist nahezu kreisförmig. Für eine Umrundung
der Milchstraße benötigt die Sonne etwa 230 Millionen Jahre.
Die Bahndaten der Sonne innerhalb der Milchstraße ermittelte man anhand von
Messungen der Radialgeschwindigkeit
von Kugelsternhaufen.
Man nützte dabei die Erkenntnisse von
Harlow Shapley, der aus der Größe und Verteilung der
Kugelsternhaufen ungefähr die Größe der Milchstraße abgeschätzt hatte.
Er wusste bereits, dass die Sonne nicht im Zentrum der Milchstraße stand.
Aus der Helligkeit von Kugelsternhaufen hatte er deren Entfernungen abgeschätzt.
Nach der Entdeckung von Cepheiden in den Kugelsternhaufen
gelangen ihm 1914 dann deren genaue Entfernungsbestimmung.
Die Rotverschiebung der Galaxien
 |
Rotverschiebung der Spektrallinien
eines weit entfernten
Supergalaxienhaufen (BAS11) rechts
im Vergleich zur Sonne links.
Bildherkunft |
In den 1920er Jahren wurde viel gerätselt über die so genannten
Spiralnebel, von denen die
Andromedagalaxie der bekannteste und auch nächste ist.
1923 fand Edwin Hubble nun Cepheiden in der Andromedagalaxie.
1925 ermittelte er daraus für die Andromedagalaxie eine Entfernung von 900000
Lichtjahren. (Heute weiß man, dass es 2,5 Millionen Lichtjahre sind.)
Wegen dieser nun nachgewiesenen großen Entfernung konnte die Andromedagalaxie
nicht mehr zur Milchstraße gehören. (Die Milchstraße hat einen Durchmesser von
100000 Lichtjahren.)
1926 veröffentlichte Hubble Entfernungen zu noch weiter entfernten Galaxien.
Damit war bewiesen, dass alle Spiralnebel eigenständige Galaxien sind, und
dass sie nicht zur Milchstraße gehören.
Die Spektren aller Galaxien - außer der Andromedagalaxie - zeigen eine
Rotverschiebung, wie wir sie beim
Doppler-Effekt oben besprochen haben.
Diese Galaxien entfernen sich von uns.
Je weiter sie entfernt sind, umso größer ist die Rotverschiebung.
Die Andromedagalaxie dagegen lässt eine Blauverschiebung erkennen.
Sie kommt auf uns zu und wird uns vielleicht in 2 Milliarden Jahren erreichen.
Aus der Rotverschiebung der Galaxien schloss
Georges Lemaître im Juni 1927 auf eine
Ausdehnung des Weltalls. Er begründete die Ausdehnung mit
den Formeln aus Einsteins
Allgemeiner Relativitätstheorie.
Lemaître hatte damit bereits die als Hubble-Gesetz bekannt gewordene Formel
v = H ⋅ r vorweg genommen - zusammen mit einem Wert
für die Hubble-Konstante H0.
Hubble selbst hat sein Gesetz erst 1929 veröffentlicht, wobei er nicht
von einer Ausdehnung des Weltalls sprach. Die Galaxien hätten sich ja auch in
ein vorhandenes Weltall ausdehnen können, etwa wie Gas in ein luftleeres
Gefäß.
1931 erschien dann Lemaîtres Artikel, in welchem er die Idee des
Urknalls
als quantenphysikalischen Beginn der kosmischen Expansion in die
Kosmologie
einführte.
Man kann sich die Ausdehnung des Weltalls vorstellen, wie die Oberfläche eines
Luftballons beim Aufblasen. Irgendwo auf dem Luftballon liegt die Milchstraße.
Die Oberfläche des Ballons dehnt sich in alle Richtungen gleichermaßen aus.
Keine Richtung ist bevorzugt.
Da das Weltall sich aber ausdehnt, dürfen wir einen Anfang annehmen, der nach
heutigem Wissen vor etwa 13,7 Milliarden Jahren geschah.
Durch die Rotverschiebung kann man nun auch die Entfernungen zu Himmelsobjekten
bestimmen, in denen man - wegen der großen Entfernung - keine Cepheiden mehr
erkennen oder optisch auflösen kann.
Aus v = H ⋅ r und
Δλ / λ0
= v / c = z folgt
r = Δλ / λ0 ⋅ c / H
oder r = z ⋅ c / H
Dabei ist r die Entfernung des Objekts in Megaparsec, wobei
1 Parsec (pc) = 3,0857e16 m = 3,261564 Lichtjahre ist.
v ist die Geschwindigkeit des Objekts in km/s, c die Lichtgeschwindigkeit in
km/s. z ist die Rotverschiebung und H die Hubble-Konstante
H ≈ (74,3 ± 2,1) km/s/Mpc.
Der angegebene Wert für H wurde mit dem
Spitzer-Weltraumteleskop gemessen. Andere haben Werte
zwischen 67 und 77 ermittelt. Die genaue Eichung ist also noch in Arbeit.
Galaxien haben nun auch die Eigenart, dass sie sich - aufgrund ihrer Masse -
gegenseitig anziehen. Dadurch bewegen sie sich aufeinander zu. Diese
Eigenbewegung von oft mehreren hundert km/s muss bei der Entfernungsmessung
nach der Rotverschiebung beachtet werden. Man misst am besten die Galaxien
der ganzen Gruppe. Dann könnten sich die Eigenbewegungen herausmitteln.
Beispielsweise müsste sich die Andromedagalaxie nach der Formel für die
Rotverschiebung mit
v = H ⋅ r ≈ 74,3 km/s/Mpc ⋅ 0,7665 Mpc
≈ 57 km/s
von uns wegbewegen. Tatsächlich fliegt sie aber mit 300 km/s auf uns zu.
Die Andromedagalaxie und die Milchstraße ziehen sich gegenseitig an.
Temperatur und Strahlungsleistung eines Sterns
Sterne haben Temperaturen zwischen etwa 3000° und etwa 25000° Kelvin.
Um sie zu verstehen, betrachtet man sie als
Schwarze Körper nach dem
Planckschen
Strahlungsgesetz.
Dieses Gesetz zeigt, mit welcher Leistung der Schwarze Körper strahlt.
Dabei wird für eine Temperatur aufgezeigt, wie viel Leistung auf jeder
einzelnen Wellenlänge abgestrahlt wird. Für jede Temperatur findet man eine
Kurve im Diagramm rechts.
Die rote Kurve ist für 300° Kelvin, also für 27° Celsius. Die Temperatur der
Sonne entspricht etwa der gelben Kurve.
Bei einem Stern mit einer Oberfläche von 3000° ist die Farbe Rot etwas stärker
vertreten, bei einem Stern von 10000° findet man mehr Blau.
Wir erkennen auch, dass die Strahlungsleistung bei höherer Temperatur ganz
gewaltig ansteigt.
Man erkennt an den Kurven des Planckschen Strahlungsgesetzes, dass zu den
Höchstwerten jeder Kurve eine bestimmte Wellenlänge λmax
(engl. Peak wavelength) gehört. Dieser Zusammenhang ist als
Wiensches
Verschiebungsgesetz bekannt:
λmax ⋅ T = 2,8978E6
[nm ⋅ K]
Man nimmt das Spektrum des Sterns und sucht dort die hellste Stelle.
Aus der Wellenlänge λmax (in nm) zu dieser Stelle
berechnet man dann die Oberflächentemperatur T des Sterns.
Von einem Stern ist nicht nur die Strahlung auf den einzelnen Wellenlängen
interessant, sondern auch die gesamte Strahlung. Berechnet man etwa die
Fläche unter einer Kurve des Planckschen Strahlungsgesetzes, so bekommt man
die Strahlungsleistung jedes Quadratmeters des Sterns. Ich bezeichne
die Größe mit F. Sie heißt auch
Spezifische Ausstrahlung oder engl. Radiant excitance.
F = σ ⋅ T4 wobei
σ = 5,67E-8 [Wm-2K-4] die
Stefan-
Boltzmann-
Konstante und T die Oberflächentemperatur
des Sterns ist.
Für die Sonne (T = 5780 K bei λmax = 501 nm) ergibt
sich die abgestrahlte Leistung jedes Quadratmeters mit F = 63,3 MW/m².
Siehe rote Linien im zweiten Bild (zum Wienschen Verschiebungsgesetz).
(°R bezieht sich auf die Rankineskala.)
Man kann man nun die gesamte Strahlungsleistung eines Sterns L oder auch
seine Leuchtkraft berechnen, indem man F mit der Oberfläche des
Sterns malnimmt:
L = F ⋅ 4π ⋅ R2 oder
L = 4π ⋅ σ ⋅ T4
⋅ R2
wobei R der Sternradius ist.
Für die Sonne (R = 6,96E8 m) ergibt sich so eine abgestrahlte Leistung
von L = 3,845E26 W.
Die Erde ist von der Sonne 1,496E11 m entfernt. Die von der Sonne
beschienene Seite der Erde bekommt also Strahlungsleistung pro Quadratmeter von
3,845E26/4/π/(1,496E11)2 =
1370 W/m2 ab.
Der Wert heißt Solarkonstante.
Etwa 30% dieser Strahlung wird von der Atmosphäre wieder reflektiert.
Ein weiterer Teil wird absorbiert. Bei senkrechter Einstrahlung von oben
ergeben sich so etwa 900 W/m2.
Wenn man die Einstrahlung der Sonne noch umrechnet auf die Oberfläche der
gesamten Erde - also auf Tag- und Nachtseite, so ergeben sich
342,5 W/m2.
Durch Reflexion und Absorption in der Atmosphäre kommen im Mittel noch etwa
240 W/m2 unten an.
Siehe auch Strahlungshaushalt der Erde.
Über Sternhelligkeiten und über die mag-Größen habe ich
oben schon geschrieben. Die Helligkeitsklassen sind so
aufgeteilt, dass ein Unterschied von 5 Klassen einem Helligkeitsunterschied
von 1:100 entspricht. Je höher die Klasse, desto schwächer die Helligkeit.
Hier wird nun die absolute
bolometrische Helligkeit betrachtet. Man kann damit die
Strahlungsleistung von Sternen vergleichen:
Mbol − Mbol Sonne = -2,5 ⋅
lg ( L / LSonne ) = -2,5 ⋅
lg ( F / FSonne )
Ein Stern mit 100facher Strahlungsleistung der Sonne hat eine um 5 mag
niedrigeren mag-Wert.
Und es gibt einen Nullpunkt:
Mbol = 0 = M0
entspricht L0 = 3,0128E28 W.
Für die Sonne (L = 3,845E26 W) ergibt sich
Mbol Sonne = 2,5 ⋅ lg ( 3,0128E28 / 3,845E26 )
= 4,735
(Mv Sonne = 4,83; liegt also in der Nähe.)
Als ein Anwendungsbeispiel zum
Stefan-Boltzmann-Gesetz rechnen wir nun den Radius des
Sirius aus.
Sirius hat eine scheinbare Helligkeit: m = -1,46;
eine Entfernung: 8,6 Lichtjahre = 2,64 pc;
eine Oberflächentemperatur: T = 9900°K;
eine Leuchtkraft 25,4±1,3 Sonnenleuchtkräfte.
Wir vergleichen nun Sirius mit der Sonne. Die Gleichungen
LSirius = 4π ⋅ σ ⋅
TSirius4
⋅ RSirius2 und
LSonne = 4π ⋅ σ ⋅
TSonne4 ⋅ RSonne2
kann man durcheinander teilen:
LSirius / LSonne = ( TSirius /
TSonne )4 ⋅ ( RSirius / RSonne
)2.
Einsetzen von Werten ergibt:
( RSirius / RSonne )2 = 25,4 /
( 9900°K / 5778°K )4 oder
RSirius / RSonne = 1,717 oder
RSirius = 1,195E6 km.
Man kann auf diese Weise Sternradien berechnen, die man mit einem Fernrohr nicht
mehr erkennen kann.
Der Winkel, unter dem der Durchmesser des Sirius von der Erde aus erscheint,
beträgt 0,006".
Das kann der 5m-Spiegel auf dem Mount Palomar nicht mehr darstellen.
Der Sirius erscheint dort als Beugungsscheibchen von 0,05" Durchmesser.
Die Entdeckung des Wasserstoffs der Sterne
Nachdem Fraunhofer die dunklen Linien im Sonnenspektrum vermessen
hatte und Gustav Kirchhoff zusammen mit
Robert Bunsen die Linien auf Gase im Lichtweg zurückführen
konnten, wusste man, dass die Materie der Sonne aus den gleichen chemischen
Elementen bestand, wie auch die Erde.
Es war nun naheliegend auch das Licht der Sterne zu untersuchen.
William Higgins und seine Frau
Margaret fertigten viele Fotos an von Spektren
verschiedener Sterne und von Nebelflecken an. Sie zeigten 1863, dass in den
Sternspektren dieselben chemischen Elemente wie auf der Erde sichtbar waren.
In planetaren Nebeln fanden sie Emissionsspektren von Gasen, und sie konnten
auch Wasserstoff nachweisen.
Auch Angelo Secci untersucht Sterne. 1867 veröffentlichte er
ein Verzeichnis von 500 Sternen, in dem er deren Spektren zunächst in drei
später in fünf Klassen einteilte. Er war der erste, der versuchte, eine Ordnung
in die enorm große Datenmenge aus den Spektren zu bekommen.
In den USA fertigte der Physiologe und Privat-Astronom
Henry Draper sehr viele Fotografien von Spektren an.
Nach seinem Tod spendete die Witwe seinen Nachlass der Harvard Universität.
Sie finanzierte auch die Herausgabe des so entstandenen
Henry-Draper-Katalogs mit 225300 Sternen in den Jahren
1918-1925.
Die Zusammenstellung des Katalogs lag bei
Edward Charles Pickering dem Leiter des Harvard College
Observatory.
Er beschäftigte für die Auswertung der unzähligen Sternspektren viele Frauen
als "Computer", also als Berechner. Anscheinend hielt man Frauen
besser geeignet für derartige fisselige Arbeiten. Diese Frauen sind als
"Pickerings Harem" bekannt geworden. Einige, darunter
Antonia Maury,
Henrietta Swan Leavitt,
Williamina Fleming und
Annie Jump Cannon,
machten viele Aufsehen erregende astronomische Entdeckungen.
Sie schufen gemeinsam in mehreren Schritten die
Harvard Spektralklassifikation.
Zuerst baute Williamina Fleming ein System auf, das die Sterne danach einstufte,
wie viel Wasserstoff in ihrem Spektrum beobachtet werden konnte.
Die Sterne wurden in Klassen A bis P eingeordnet.
Annie Cannon entwickelte daraus eine einfachere Klassifikation aufgrund der
Temperatur - das Wiensche Verschiebungsgesetz (siehe oben)
war ja seit 1893 bekannt. Williamina Flemings Zuordnung der Buchstaben zu den
Klassen wurde beibehalten. Nur die Reihenfolge der Buchstaben wurde geändert.
Die Reihenfolge der Spektralklassen ist nun O, B, A, F, G, K und M.
Annie Cannon schuf dafür den Merksatz Oh, Be A
Fine Girl - Kiss Me!.
Sie führte auch Nummern zur weiteren Unterteilung einer Spektralklasse in
einzelne Spektraltypen ein, wobei eine höhere Zahl einer geringeren Temperatur
entspricht. Die Sonne ist etwa ein Stern mit Spektraltyp G2. Sie ist
damit kühler als ein Stern des Typs G1, jedoch wärmer als ein Stern des
Spektraltyps G3.
Später kamen noch weitere Klassen hinzu.
Dann kam aus England
Cecilia Payne (verheiratete Payne-Gaposchkin) nach Harvard.
In England hatte sie Astronomie studiert, durfte aber dort als Frau keinen
Abschluss machen. In Harvard durfte sie jedoch im für Frauen reservierten
Radcliffe College 1925 ihre
Doktorarbeit abgeben.
Zeitgenossen sagten, es sei die beste Doktorarbeit gewesen, die in Astronomie
jemals geschrieben wurde. Es dauerte aber bis 1956, bis sie als erste Frau
Professor für Astronomie in Harvard wurde.
Cecilia Payne konnte in ihrer Arbeit den Sternen der einzelnen Spektralklassen
genau eine Temperatur zuordnen. Sie benützte dazu die Ionisations-Theorie
des Indischen Physikers Meghnad Saha. Dann zeigte sie, dass die enorme Vielfalt
der stellaren Absorptionslinien abhängig vom Ionisationsgrad bei verschiedenen
Temperaturen ist, und dass diese Vielfalt nicht abhängig von der Menge der
Elemente ist.
Sie wies nach, dass Silizium, Kohlenstoff und die anderen üblichen Elemente,
die man im Spektrum der Sonne erkennt, in den Sterne etwa in gleichem Verhältnis
vorkommen, wie auf der Erde. Das entsprach auch dem damaligen Annahmen.
Jedoch erkannte sie, dass Helium und vor allem Wasserstoff in weit größeren
Mengen in den Sternen vorhanden sind als auf der Erde - bei Wasserstoff etwa
eine Million Mal mehr. Damit war Wasserstoff als der Hauptbestandteil der
Sterne und somit als das häufigste Element im Weltall erkannt worden.
(Siehe auch
Liste der Häufigkeiten chemischer Elemente.)
Kirchhoff und Bunsen haben festgestellt, welche Vielfalt an Elementen überhaupt
in leuchtenden Gasen enthalten sein kann.
Cecilia Payne hat uns auch die Mengen bestimmt. Allein aus seinem Licht
kann man nun bei einem Stern sagen, woraus er besteht, wie heiß er ist,
wie stark er strahlt.
Aber das ist noch nicht alles, was man aus dem Spektrum lesen kann.
Die folgenden Kapitel zeigen uns, wie schwer ein Stern ist, wie groß er ist,
wie alt er ist, wie lange er noch strahlt, wie er stirbt.
Das Hertzsprung-Russell-Diagramm
Die Erkenntnis, dass die Objekte am Himmel - sofern es sich um Fixsterne
handelt - in Wirklichkeit Sonnen sind, hat sich schon lange durchgesetzt.
Offensichtlich sind diese Sterne aber nicht gleich. Sie haben unterschiedliche
Farben - folglich auch unterschiedliche Oberflächentemperaturen.
Wenn man dann noch ihre Entfernung kennt, kann man auch die unterschiedlichen
Leuchtkräfte und damit die unterschiedlichen Radien berechnen.
Es stellt sich die Frage: Kann man die Sterne eigentlich irgendwie in Gruppen
ordnen? Kann man etwas über die Häufigkeit in diesen Gruppen sagen?
Bereits 1909 arbeitete Ejnar Hertzsprung an einem Temperatur-Leuchtkraft-Diagramm
bei Sternen. Er erkannte, dass bei gleicher Oberflächentemperatur Riesensterne
und Zwergsterne auftreten können.
Henry Norris Russell und andere Astronomen entwarfen
unabhängig davon ähnliche Diagramme.
Anfangs beschränkte man sich auf
Offene Sternhaufen, da deren Sterne alle eine nahezu gleiche
Entfernung von uns haben. Deshalb konnte man ihre Helligkeiten auch direkt
miteinander vergleichen.
Heute kann man die
Hertzsprung-Russell-Diagramme für jedes Sternengebiet
angeben. Sie waren ein ganz besondere wissenschaftliche Erkenntnis.
Das Bild zeigt uns einige bekannte Sterne aus unserem Himmel als Beispiele.
In Wirklichkeit sind es enorm viel mehr Sterne.
In den farbigen Bereichen des Diagramms kommen besonders viele Sterne
vor; in den schwarzen Bereichen findet man fast keine. Beispielsweise gibt es
kaum einen roten Stern von der Masse und der Leuchtkraft unserer Sonne.
Auf der x-Achse sind zur Orientierung auch die Spektralklassen (O-M)
eingetragen. Die Farben dienen dabei nur zur Orientierung. Ein Stern mit
T = 30000 K strahlt am meisten im Ultraviolett und erscheint uns
am Himmel weiß mit leichtem Blaustich. Ein Stern von T = 3000 K
strahlt besonders im Infrarot und erscheint uns am Himmel rötlich.
Auf der y-Achse sehen wir die Leuchtkraft in Vielfachen der
Sonnenleuchtkraft. Beide Achsen sind im logarithmischen Maßstab.
Die grauen Linien zeigen uns Sterne von gleichem Radius. Der Radius
ergibt sich aus dem Stefan-Boltzmann-Gesetz
L = 4π ⋅ σ ⋅ T4 ⋅
R2
wobei R der Sternradius, L die Leuchtkraft und T die
Oberflächentemperatur ist.
Die Größen der Kugeln für die Beispielsterne ist annähernd logarithmisch
gezeichnet und sie dienen zur Orientierung. Anhand der grauen Linien kann man
die wahre Größe dieser Sterne abschätzen. Siehe auch Objekte
der Astronomie oben.
Wer die exakten Werte über die Sonne wissen will: R = 696342 km;
L = 3,846E26 W; T = 5778 K;
M = 1,9884E30 ± 2E26 kg.
Bestimmte Gebiete im Hertzsprung-Russell-Diagramm haben besondere Namen:
Es sind das die Hauptreihe, das Gebiet der
Riesen und Überriesen und die
Weißen Zwerge.
Zuerst möchte ich erklären, was man in den Gebieten vorfindet. Erst später
möchte ich den Weg der Sterne durch die Gebiete aufzeigen, den die Stern im
Laufe ihren Lebens dort zurücklegen.
Die Hauptreihe
Die Hauptreihe ist dies ein balkenförmiges Gebiet
von links oben (Beta Centauri) bis rechts unten (Proxima Centauri).
Auch die Sonne ist in der Mitte eingezeichnet.
Die Breite des Balkens im Diagramm sagt nichts über die Anzahl der Sterne dort
aus, sondern zeigt uns nur die Streuung der enorm vielen dort gefundenen
Sterne.
Die meiste Zeit seines Lebens verbringt ein Stern in der Hauptreihe.
Er gelangt dort hin nach dem Zünden der Kernfusion. Sobald der Stern nun
Wasserstoff verbrennt, und das ist ein lange
dauernder und relativ stabiler Zustand, solange bleibt er in der Hauptreihe.
Im Innern des Sterns drückt der
Schweredruck nach unten. Dem wirkt der durch
die hohe Kerntemperatur erzeugte
Gasdruck zusammen mit dem
Lichtdruck entgegen. Wenn sich der Druck auf
diese Weise ausgleicht, haben wir ein stabiles System.
Nur am Anfang - auch schon vor dem Zünden - zeigt der Stern teilweise starke
Ausbrüche. In dieser T-Tauri-Phase wird durch den starken Sonnenwind der Staub
aus dem jungen Planetensystem weggeblasen.
Im Laufe seiner Zeit auf der Hauptreihe steigt der Stern etwas auf der
Hauptreihe nach oben. Unsere Sonne strahlte vor 1 Milliarde Jahren nur mit etwa
70% ihrer heutigen Leuchtkraft.
In 500 Millionen Jahren wird sie ein klein wenig heller strahlen - leider wird
dann die Erde wegen der erhöhten Temperatur nicht mehr bewohnbar sein.
Im Diagramm findet man neben der Hauptreihe das Kürzel Mson.
"60 Mson" bezeichnet dabei einen Stern mit 60 Sonnenmassen.
Die Angabe ist ein Richtwert, der sich nur auf Sterne der Hauptreihe
links oder rechts von dem Kürzel bezieht.
Für 0,5 Msonne <= M <= 10 Msonne gilt:
L / Lsonne = (M / Msonne) ** 3,5.
Die Massen bekam man aus der Untersuchung von
Doppelstern-Systemen.
Man findet neben der Hauptreihe auch Angaben über die Lebensdauer von
Sternen.
Wir erkennen, dass Sterne von über 10 Sonnenmassen nur 10 Millionen Jahre
leben. Die Sonne hat aber 10 Milliarden Jahre zur Verfügung. Dagegen strahlt
der Stern mit 10 Sonnenmassen 10000 mal so stark wie die Sonne.
Große Sterne sind sehr verschwenderisch mit ihrem Brennvorrat.
Diese kurze Lebensdauer kann nun zur Altersbestimmung von
Sternhaufen verwendet werden. Sternhaufen sind klar
abgegrenzt vom Rest der Galaxis. Man hat nun von den Sternen eines Sternhaufens
ein Herzsprung-Russell-Diagramm angefertigt. Dabei hat man festgestellt, dass
die obere linke Hauptreihe kaum besetzt ist - es sind dort nur ganz wenig
Sterne.
Daraus folgt, dass es seit etlichen Milliarden Jahren dort keine Sternentstehung
mehr gegeben hat - von einigen wenigen Nachzüglern mal abgesehen.
Aus solchen Untersuchungen weiß man, dass Kugelsternhaufen typischerweise
12,7 Milliarden Jahre alt sind. Offene Sternhaufen dagegen meist nur
10 Millionen Jahre.
Das Universum selbst ist 13,7 Milliarden Jahre alt. (Siehe
Rotverschiebung.) Da Sterne von 0,1 Sonnenleuchtkraft
(etwa 61_Cygni) 100 Milliarden Jahre leben, so kann man noch keine
Sternleichen dieser Rote Zwerge auffinden.
Die Angaben zur Lebensdauer im Bild oben sind nur Richtwerte für die Zeit nach
dem Zünden des Wasserstoffbrennens bis zum Übergang zur Sternleiche.
Über die Lebensdauer dieses letzten Leichenzustands ist nichts ausgesagt.
Die Riesen und Überriesen
Nachdem wir nun die Hauptreihe besprochen haben kommen wir zum Gebiet der
Riesen rechts oben im Diagramm.
Massereichere Sterne (M > 0,26 Msonne) gelangen nach dem Hauptreihen-Stadium
in das Gebiet der Riesen oder Überriesen. Sterne mit weniger Masse kommen gar
nicht in dieses Gebiet, sondern enden nach der Hauptreihe als
Weiße Zwerge.
Beim Wasserstoffbrennen sammelt sich im Kern des Sterns immer mehr Helium an.
Der Wasserstoff um diesen Kern brennt aber in einer Kugelschale weiter.
Der Gasdruck im Heliumkern nimmt ab, weil keine Fusion mehr abläuft.
Nun presst der Schweredruck das Helium zusammen und dessen Temperatur steigt.
Durch diese enorme Erhitzung dehnt sich der Stern aus. Sein Radius steigt auf
das mehr als 100fache. Im Diagramm wandern die Sterne nach rechts.
Sind im Kern 100 Millionen Grad erreicht, so zündet dann auch das
Helium im Kern. Außerhalb des Kerns brennt der Wasserstoff
als Schale weiter.
Das Heliumbrennen ist kein besonders stabiler Vorgang. Er ist extrem
temperaturabhängig. Deshalb kann der Stern während des Heliumbrennens
schon mal Teile seiner Hülle einfach abstoßen.
Wenn im Kern das Helium verbraucht ist, und wenn eine genügend hohe Temperatur
dort erreicht wird (500-900 Millionen K), beginnt im Kern das
Kohlenstoffbrennen. Über dem Kern brennt nun eine
Heliumschale, darüber die Wasserstoffschale.
Bei jedem Zünden eines Elements, sei es nun Helium oder Kohlenstoff, kann ein
Teil der äußeren Hülle des Sterns weggesprengt werden. Der Massenverlust muss
nicht groß sein. Dann kann das Kernbrennen für einige Zeit ausgehen und wieder
kommen.
In anderen Fällen kann der Stern beim Zünden eines neuen Elements gänzlich
explodieren. Wenn im Kern aber die Temperatur für das Zünden nicht erreicht
wird, so dehnt sich doch die Hülle weiter aus.
Übrig bleibt am Ende meist ein
Planetarer Nebel und in der Mitte ein
Weißer Zwerg.
Bei sehr massereichen Sternen (M > 8 Msonne) und bei entsprechend hoher
Temperatur brennt nach dem Kohlenstoff das Neon, der Sauerstoff und schließlich
das Silizium. Dieses Schalenbrennen endet, wenn im Kern Eisen überwiegt.
Eisen kann nicht weiter verbrannt werden.
Die äußeren Schalen drücken dann nach unten und haben keinen Gegendruck mehr.
Die Gravitationsenergie der Schalen ist so hoch, dass der Stern als
Typ-IIP-Supernova explodiert.
Am Ende bleibt eine Sternleiche übrig - in Form eines
Weißen Zwergs, eines
Neutronensterns (wenn Restmasse > 1,4 Msonne) oder eines
Schwarzen Lochs (wenn Restmasse > 3 Msonne).
Riesen hat man auch in Kugelsternhaufen gefunden. Wegen ihrer hohen Leuchtkraft
kann man sie sogar von ihrer Umgebung unterscheiden. Durch Vergleich mit
entsprechenden Riesen in der Milchstraße konnte man in den 1910er Jahren sogar
die ungefähren Entfernung der Kugelsternhaufen angeben.
Anmerkung:
Die angegebenen Zahlen sind aufgrund von Modellrechnungen entstanden.
Die Werte sind rein theoretisch und auch noch sehr ungenau.
Beobachtungen am Himmel gibt es kaum - wann explodiert schon mal ein Stern.
Eigentlich müsste man noch viele weitere Parameter für eine genauere Aussage
berücksichtigen - etwa Rotationszeit des Sterns, Zusammensetzung (Population I
oder II), spektrale Besonderheiten, Anzahl und Stärke der Ausbrüche als
Veränderlicher Stern.
Die Weißen Zwerge
Die Weißen Zwerge ist ein Gebiet links unten
im Hertzsprung-Russell-Diagramm.
Ein Weißer Zwerg bleibt übrig, wenn ein Roter Riese seine Hüllen abgestoßen hat.
Beim Abstoßen der Hülle muss die Restmasse unter 1,44 Sonnenmassen liegen,
sonst entsteht Neutronenstern, oder ab 2,5 Sonnenmassen ein Schwarzes Loch.
Für ein Schwarzes Loch muss der Vorgänger mehr als 8 Sonnenmassen gehabt haben.
Schwarze Löcher und Neutronensterne sind selten, da die Restmasse eines
Riesensterns selten über 1,44 Sonnenmassen liegt.
Bei den bisher gefundenen Weißen Zwergen liegt deren Masse zwischen
0,4 und 1,1 Sonnenmassen, wobei 90% bei 0,5 bis 0,7 liegen.
Die Leuchtkraft der hellsten Weißen Zwerge kann die 10fache Sonnenleuchtkraft
haben. Die Oberflächentemperatur liegt dann bei 65000 K.
Da in einem Weißen Zwerg keine Fusion oder ein weiteres Zusammenziehen der
Materie stattfindet kühlt er über die Jahrmilliarden ab. Einer der kühlsten
Weißen Zwerge hat nur noch 1E-4 Sonnenleuchtkräfte und 4000 K.
Weiter konnte er sich in der Zeit der Existenz des Universums noch nicht
abkühlen.
Weiße Zwerge haben Radien von 7000 bis 14000km (1-2 Erdradien). Unsere Sonne
hat 700.000km. Die Dichte, etwa 1 Tonne pro cm³ oder 1E10 kg/m³ ist
unvorstellbar hoch. Es handelt sich um
entartete Materie, die nur quantenmechanisch erfassbar ist.
Der Druck im Zentrum beträgt 2,5E22 N/m², das Millionenfache über dem zentralen
Sonnendruck.
Wegen ihrer geringen Leuchtkraft sind nur Weiße Zwerge in der Umgebung der
Sonne bekannt. Aber wegen der statistischen Anzahl pro Kubiklichtjahr schätzt
man, dass etwa 10% aller Sterne Weiße Zwerge sind.
Neutronensterne und
Schwarze Löcher findet man im Hertzsprung-Russell-Diagramm
nicht.
Neutronensterne haben typischen Radien von etwa 10,4 bis 11,9 km, also
1000 Mal kleiner als Weiße Zwerge. Ihre Massen liegen zwischen etwa 1,2 und 2,0
Sonnenmassen. Ihre Dichte nimmt von etwa 1E9 kg/m³ an ihrer Kruste mit der
Tiefe bis auf etwa 8E17 kg/m³ zu, also dreimal dichter als ein Atomkern.
Es sind die dichtesten bekannten Objekte ohne Ereignishorizont.
Die Temperatur im Inneren eines Neutronensterns beträgt anfangs 100 Milliarden
Kelvin, die durch Abstrahlung von Neutrinos innerhalb eines Tages auf ca. eine
Milliarde Kelvin sinkt. Innerhalb von ca. 100 Jahren sinkt die Temperatur auf
ca. 300.000 Kelvin. Erst nach etwa 100.000 Jahren tragen emittierte Photonen
mehr als Neutrinos zum Temperaturrückgang bei. Nach einer Million Jahren werden
10.000 Kelvin unterschritten.
Neutronensterne strahlen also nicht lange im sichtbaren Licht.
Sie sind selten.
Schwarze Löcher sind noch seltener als Neutronensterne.
Die ersten Sterne bildeten sich aus Wasserstoff- und Heliumgas
200 Millionen Jahre nach dem Urknall. Diese
Population-III-Sterne waren 100 bis 1000 Mal so schwer wie
die Sonne. Sie hatten bei einer Oberflächentemperatur von 100.000 Grad eine
Leuchtkraft 1-30 Millionen Mal so stark wie die der Sonne.
Deshalb war die Lebensdauer dieser Sterne nur etwa 2-3 Millionen Jahre.
Am Ende explodierten sie in einer
Supernova, und es bildeten sich die chemischen Elemente
bis zum Uran. Die Elemente wurden im All verteilt.
Übrig blieben Schwarze Löcher. Man kann annehmen, dass diese sich vereinigten
und dann die Zentren der Galaxien bildeten.
Sternentstehung
Bitte beachten Sie die Anmerkung oben.
Die Sternentstehung beginnt mit einer
Wolke aus Molekülen und Staub.
Diese Wolke ist etwa 100 bis 1000 Lichtjahre groß und hat eine Masse von 10000
bis zu 10 Millionen Sonnenmassen.
Wenn sie kalt genug ist (etwa 10 K), kann sie sich zusammenziehen.
(Siehe auch Jeans-Kriterium.)
Da die Wolke nicht überall gleich dicht ist, entstehen an mehreren dichteren
Stellen im Laufe von Jahrmillionen mehrere hundert oder gar tausende Sterne
in einem Offenen Sternhaufen, der sich wahrscheinlich nach
einigen hundert Millionen Jahren in freie Einzel- oder Doppelsterne
auflöste. 60-70% sind dabei Doppel- und Mehrfachsterne.
Wenn sich eine dichtere Stelle der Wolke zusammenzieht, so fängt sie immer mehr
Materie ein. Die Mitte heizt sich durch die
Gravitationsenergie immer mehr auf.
Außerhalb der Verdichtung sieht man den Protostern allerdings
noch nicht, denn der Staub verdunkelt den neuen Stern noch.
Sobald der Kern über 1000 K heiß ist und alle Atome ionisiert sind, strahlt der
Stern und pustet mit seinem Sonnenwind den Staub um die inneren Protoplaneten
hinweg. (T-Tauri-Phase). Der Protostern kann sich dann weiter
verdichten, bekommt aber von außen keine Materie mehr.
Es dauert mehrere Millionen Jahre, bis das Innere des Sterns für eine
Kernfusion heiß genug ist.
Wie sich ein Objekt nun weiter entwickelt, hängt von seiner Masse ab.
Braune Zwerge
Ab 0,012 Sonnenmassen oder 13 Jupitermassen kann eine
Deuteriumfusion stattfinden.
Solche Objekte nennt man Braune Zwerge. Kleinere Objekte, bei denen noch keine
Fusion erfolgt, nennt man
Objekte planetarer Masse.
Da Braune Zwerge nur sehr schwach (unter 1E-4 Sonnenleuchtkräften) im Infrarot
strahlen, sind sie nur schwer auffindbar. Ihre Oberflächentemperatur liegt
unter 2700 K. In der Entstehungsphase können sie 2900 K erreichen.
Braune Zwerge sind wahrscheinlich sehr zahlreich - es gibt vielleicht
100 Milliarden in der Milchstraße.
Rote Zwerge
Ab 0,07 Sonnenmassen oder 75 Jupitermassen oder 1,39E29 kg spricht man von
einem
Stern.
Bei dieser Masse findet im Innern das
Wasserstoffbrennen, eine Wasserstoff-Kernfusion, statt.
Die kleinsten dieser Sterne, bis zu 0,6 Sonnenmassen, nennt man
Rote Zwerge.
Sie strahlen nur mit 0,0001-0,05 der Sonnenleuchtkraft bei
Oberflächentemperaturen von 2500-4000 K. Deshalb bleiben sie mehrere
10 Milliarden bis zu Billionen Jahren in der Hauptreihe.
Sie sind heute immer noch dort.
Es wird bei den Roten Zwergen kein Heliumbrennen und kein Riesenstadium geben.
Sie werden als Weiße Zwerge enden.
Etwa 3/4 aller Sterne sind Rote Zwerge.
Unsere Sonne
Die Sterne der Spektralklasse G sind der Sonne sehr ähnlich.
Man nennt sie Gelbe Zwerge. Ihre Oberflächentemperatur beträgt
5300 bis 6000 K bei 0,8 bis 1,1 Sonnenmassen.
Ein gelber Zwerg verweilt während seiner Existenz ca. 10 Mrd. Jahre in der
Hauptreihe.
Die Entwicklung unserer Sonne soll hier anhand des
entsprechenden Ausschnitts aus dem Wikipedia-Artikel über die
Sonne als
stellvertretendes Beispiel dargestellt werden. Im Folgenden habe ich eine
verkürzte Fassung zusammen gestellt.
Die Daten für die Entwicklung der Sonne sind aus Modellrechnungen
entstanden.


Oberes Bild:
Bildherkunft;
Unteres Bild:
Bildherkunft
Der untere blaue Balken zeigt das letzte Prozent der Entwicklungszeit der Sonne.
Die Temperaturen im gelben Balken gelten für die Erdoberfläche.
Die Sonne als Protostern
| Phase | Dauer in
Millionen
Jahren |
Leuchtkraft | Radius |
|---|
| Hauptreihe |
11000 |
0,7 ... 2,2 | 0,9 ... 1,6 |
| Übergangsphase |
700 |
2,3 | 1,6 ... 2,3 |
| Roter Riese |
600 |
2,3 ... 2300 | 2,3 ... 166 |
| Heliumbrennen |
110 |
44 | etwa 10 |
| He-Schalenbrennen |
20 |
44 ... 2000 | 10 ... 130 |
| Instabile Phase |
0,4 |
500 ... 5000 | 50 ... 200 |
Übergang zu
Weißem Zwerg |
0,1 |
3500 ... 0,1 | 100 ... 0,08 |
Die Leuchtkraft ist in heutigen Sonnenleuchtkräften
angegeben.
Der Radius ist in heutigen Sonnenradien angegeben. |
Das Sonnensystem entstand vor 4,6 Milliarden Jahren aus einer
interstellaren Gaswolke, die sich unter ihrem eigenen
Gewicht zusammen zog. Heute ist die Sonne ein
Gelber Zwerg, der sich in einen
Roten Riesen verwandeln wird und nach etwa 12,5 Milliarden
Jahren als Weißer Zwerg enden wird.
Wir nehmen an, dass die Sonne in einem
offenen Sternhaufen zusammen mit anderen Sternen entstand.
Der Sternhaufen löste sich innerhalb von etwa 100 Millionen Jahren auf. Die
Sterne verteilten sich über die Milchstraße. Ein weiterer Sterne aus dem
damaligen Sternhaufen könnte HD 162826 sein, welcher der Sonne chemisch sehr ähnlich
ist.
Wenn sich eine dichtere Stelle der Wolke zusammenzieht, so fängt sie immer mehr
Materie ein. Die Mitte heizt sich durch die
Gravitationsenergie immer mehr auf.
Sobald der Kern über 1000 K heiß ist und alle Atome ionisiert sind, strahlt der
Stern und pustet mit seinem Sonnenwind den Staub um die inneren
Protoplaneten hinweg
(T-Tauri-Phase).
Es dauert mehrere Millionen Jahre, bis das Innere des Sterns für eine
Kernfusion heiß genug ist.
Die Sonne auf der Hauptreihe
In den folgenden 10 Millionen Jahren hat sich der innere Aufbau der Sonne
stabilisiert. Die Sonne ist nun auf der Hauptreihe angekommen.
Dort bleibt sie elf Milliarden Jahre.
In dieser Zeit steigt die Leuchtkraft auf das Dreifache - vom 0,7-fachen der
heutigen Sonnenleuchtkraft auf das 2,2-fache. Der Radius steigt auf fast das
Doppelte - vom 0,9-fachen des heutigen Sonnenradius auf das 1,6-fache.
Im Alter von 5,5 Milliarden Jahren, das heißt in 0,9 Milliarden Jahren,
überschreitet die mittlere Temperatur auf der Erdoberfläche den für höhere
Lebewesen kritischen Wert von 30°C. Eine weitere Milliarde Jahre später werden
100°C erreicht.
Schon in 500 Millionen Jahren ist die Erde für Menschen gänzlich nicht mehr
bewohnbar.
Im Alter von 9,4 Milliarden Jahren wird der Wasserstoff im Sonnenzentrum knapp.
Die Fusionszone verlagert sich in einen schalenförmigen Bereich um das Zentrum, und sie verlagert sich im Laufe der Zeit immer weiter nach außen.
Das führt jedoch zunächst nicht zu einer Veränderung des Äußeren der Sonne.
Die Übergangsphase
Wenn die Sonne 11 bis 11,7 Milliarden Jahren alt geworden ist, so verdichtet
sich die ausgebrannte Kernzone aus Helium. Dadurch steigt die Temperatur und
die Wasserstoffschale brennt stärker. Folglich wächst der Sonnenradius auf
das 2,3-fache des heutigen Sonnenradius an. Die Sonne wird rötlicher.
Sie entfernt sich von der Hauptreihe.
Die Sonne als Roter Riese
Bei einem Alter von 11,7 bis 12,3 Milliarden Jahren steigt die Leuchtkraft
der Sonne auf das 2300-fache der heutigen Leuchtkraft, der Radius auf das
166-fache des heutigen Radius. Die Sonne wird rot. Venus und Merkur fallen in
die Sonne. Die Erdkruste wird zu einem Lava-Ozean.
Durch die geringe Gravitation an der Sonnenoberfläche verliert die Sonne in
dieser Phase 28% ihrer Masse durch Sonnenwind.
Wegen der geringeren Sonnenmasse sinkt die Anziehungskraft auf die Planeten,
so dass deren Bahnradien um jeweils 38% zunehmen.
Heliumbrennen
Im Kern der Sonne gibt es nun keine Fusionen mehr. Der Schweredruck verdichtet
den Kern, bis er etwa 1E6 g/cm3 erreicht - das 10000-fache des heutigen Wertes.
Die Temperatur steigt dort schließlich auf 1E8 K.
Bei dieser Temperatur kann die Fusion von
Helium zu Kohlenstoff starten.
Gewöhnlich würde die dabei freiwerdende Energie zu einer Ausdehnung des Kerns
führen, und die Temperatur würde nicht weiter steigen.
Die Kernzone ist jedoch
entartet - sie kann sich nicht ausdehnen, aber die
Temperatur kann steigen. Die Fusion wird deshalb so heftig, dass die
Sonnenleistung für mehrere Sekunden auf 1E10 der heutigen Leuchtkraft erreicht.
Das ist etwa 10% der Leuchtkraft der gesamten Milchstraße. Erst wenn 3% des
Heliumvorrats verbrannt ist, wird die Entartung aufgehoben, und der Kern kann
sich ausdehnen.
Diese Explosion - man bezeichnet sie als den
Helium-Blitz - findet nur im Kern statt und ist äußerlich
zunächst nicht bemerkbar. Der Helium-Blitz drückt die Brennschale des
Wasserstoffs weiter nach außen. Deren Temperatur nimmt ab, und sie brennt viel
schwächer.
Es erscheint widersinnig, aber als äußerliche Folge des Helium-Blitzes sinkt
die Leuchtkraft innerhalb der nächsten 10000 Jahre auf ein Hundertstel.
In der nächsten Million an Jahren schwanken die Sonnenparameter auf und ab.
Sie pendeln, bis sich ein stabiler Zustand der Heliumfusion im Zentrum
eingestellt hat.
Das Heliumbrennen dauert 110 Millionen Jahre. Dabei wandert auch die Brennschale
des Wasserstoffs weiter nach außen. Die Leuchtkraft bleibt nahezu dauernd beim
44-fachen der heutigen Sonnenleuchtkraft und der Radius beim 10-fachen des
heutigen Sonnenradius.
Helium-Schalenbrennen
Wenn im Kern sich immer mehr Kohlenstoff sammelt, und schließlich das Helium
verbraucht ist, so beginnt das Heliumschalen-Brennen. Es dauert 20 Millionen
Jahre.
Über dem Kohlenstoff-Kern brennt nun eine Heliumschale, darüber brennt die
Wasserstoffschale.
Der Kohlenstoff im Kern wird wieder zusammen gedrückt und erhitzt sich.
Wieder steigt die Leuchtkraft - diesmal auf das 2000-fache der heutigen
Sonnenleuchtkraft. Der Radius steigt auf das 130-fache des heutigen
Sonnenradius. (Siehe auch Bild oben.)
Gegen Ende verliert die Sonne dabei einen Massenanteil von 0,1 der heutigen
Sonnenmasse.
Nach dem Schalenbrennen des Helium wird es kein
Kohlenstoffbrennen geben.
Die Sonne hat dafür zu wenig Masse.
Instabile Phase
Das Heliumbrennen ist an sich sehr temperaturabhängig. Bei höherer Temperatur
steigt es gewaltig an. Bei niedrigerer Temperatur kann es sogar aufhören.
Da im Laufe des Helium-Schalenbrennens der Kern immer mehr Kohlenstoff
aufsammelt, und weil dort keine Fusion mehr erfolgt, wird der Kern durch den
Schweredruck immer heißer. Dadurch wird die Heliumschale erhitzt.
In den letzten 500000 Jahren des Helium-Schalenbrennens erwartet man deshalb
starke Veränderungen der Sonne.
Wegen der Erhitzung der Heliumschale durch den Kern wird auch die Fusion in der
Heliumschale enorm verstärkt. Die Leistung dort erhöht sich auf etwa das
Millionenfache der heutigen Sonnenleuchtkraft. Es entsteht ein Heliumblitz.
Als Folge dehnt sich die Brennschale des Wasserstoffs aus und nimmt der
Heliumschale viel Energie weg - ihre Temperatur sinkt. Das Heliumbrennen kann
danach sogar für 200 Jahre unterbrochen werden.
Wenn man die Sonne von Außen betrachtet, so wird sich nach dem Heliumblitz
zunächst die Leuchtkraft verringern - wegen der Vergrößerung der
Wasserstoffschale.
400 Jahre später kommt die Energie des Heliumblitzes auf der Oberfläche an.
Die Leuchtkraft steigt und sinkt in den folgenden 10000 Jahren wieder ab.
Sie ändert sich zwischen dem 500- und 5000-fachem der heutigen Leuchtkraft und
der Radius zwischen dem 50- und 200-fachem des heutigen.
Solch ein Heliumblitz mit anschließenden Abklingen kann alle 100000 Jahre
erfolgen. Man erwartet vier solche Heliumblitze.
Die Sonne stößt in diesem Zeitraum von 500000 Jahren etwa 5% der heutigen
Sonnenmasse ab.
In dieser Phase wird die Sonnenoberfläche die heutige Erdbahn erreichen.
Da der Erdbahndurchmesser inzwischen größer geworden ist, könnte die Erde
noch da sein.
Übergang zum Weißen Zwerg
Am Ende der gerade beschriebenen instabilen Phase hat die Sonne ihre ganze
äußere Hülle - auch die Brennschalen für Wasserstoff und Helium - abgestoßen.
Etwa 100000 Jahre nach dem letzten Heliumblitz wird so der heiße innere Kern
sichtbar. Er besteht hauptsächlich aus hochverdichtetem Kohlenstoff und
Sauerstoff.
Dieser Kern hat nur noch einen Radius von 8% des heutigen Sonnenradius.
Seine Leuchtkraft ist am Anfang das 3500-fache der heutigen Sonnenleuchtkraft.
Seine Oberflächentemperatur ist mit 120000 K sehr hoch - er strahlt im
Ultraviolett. Dadurch bringt er die abgestoßenen Gaswolken zum Leuchten.
Es bildet sich ein
planetarischer Nebel. Durch das Verflüchtigen des Gases
erlischt diese Erscheinung nach einigen 10000 Jahren wieder.
Im Zentrum bleibt ein Weißen Zwerg.
Er hat etwa die Größe der Erde, aber eine Masse von 0,55 der heutigen
Sonnenmasse und eine Dichte von etwa einer Tonne pro Kubikzentimeter.
Da er nicht mehr fusioniert, strahlt er nur noch seine eigene Wärme ab, und
seine Temperatur sinkt nur noch.
Nach etwa 10 Millionen Jahren hat die Sonne nur noch 10% der ursprünglichen
Leuchtkraft und über mehrere 10 Milliarden Jahre wird sie zum
Schwarzer Zwerg.
Energiebilanz
Als sich die Gaswolke zusammen zog und als dabei die Kugel der Sonne entstand,
wurde eine Energie von etwa 2,3E41 J frei.
(Siehe Formel)
Die Sonne strahlt heute mit 3,846E26 W. Sie hätte mit dieser Leistung
allein aus der Gravitationsenergie theoretisch über 18 Millionen Jahre
brennen können.
Schätzt man grob, dass die Sonne 10 Milliarden Jahre brennt, bei einer mittleren
Leistung wie heute, so kommt man auf insgesamt etwa 1,2E44 J als
Strahlungsenergie, die durch Kernfusion entstehen.
Da der Massendefekt des Wasserstoffbrennens ungefähr bei 1% liegt, wird 10% der
Sonnenmasse in Helium umgewandelt.
Massenverlust durch Umwandlung in Energie 1 Promille.
28% ihrer Masse verliert die Sonne in der Phase als Roter Riese durch
Sonnenwind.
Beim Schalenbrennen verschwinden wieder etwa 10% der heutigen Sonnenmasse,
in der Instabilen Phase ungefähr weitere 5%.
Am Ende ist ein Weißer Zwerg von etwa 55% der ursprünglichen Sonnenmasse
übrig.
Nehmen wir an, die Sonne würde ihre Masse nicht verkleinern und würde von ihrem
heutigen Radius auf die Größe eines Weißen Zwergs
schrumpft, werden allein aus der Gravitationsenergie des Schrumpfens etwa
1,6E43 J frei - das ist etwa 10% des gesamten Wasserstoffbrennens.
Die Massenverluste durch Sonnenwind in den Phasen vom Roten Riesen zum Weißen
Zwerg würden diese Schrumpfenergie grob auf die Hälfte erniedrigen.
Ein Neutronenstern hat nur einen Radius von etwa 10 km, nicht 10000 km wie ein
Weißer Zwerg. Wenn am Ende ein Neutronenstern entstehen könnte, dann wäre die
Gravitationsenergie beim Schrumpfen 1000-fach größer.
Die Strahlungsenergie des ursprünglichen Sterns hätte beim Wasserstoffbrennen
dann aber auch etwas größer sein müssen.
Blaue Riesen
Links oben in der Hauptreihe findet man die
Blauen Riesen.
Diese Sterne gehören zur Spektralklasse O oder B, haben also
Oberflächentemperaturen von 30000 bis 40000 °K und strahlen
damit hauptsächlich im ultravioletten Bereich des Spektrums.
Sie haben ein 10- bis 50-fache Sonnenmasse.
Größere Sterne können sich nur in besonderen Ausnahmefällen bilden. Bei mehr
als 60 Sonnenmassen wird die Temperatur und der interne
Strahlungsdruck so groß, dass sich der Protostern nicht
weiter zusammenziehen kann.
Wegen ihrer hohen Leuchtkraft - etwa das 10.000- bis 1.000.000-fache der Sonne -
ist das Wasserstoffbrennens bereits in etwa 10 Millionen
Jahren zu Ende.
Gegen dessen Ende blähen sie sich auf, weil die Temperatur immer mehr steigt.
Sie werden zu Roten Überriesen. Im Diagramm wandern die Sterne nach
rechts.
Das Heliumbrennen beginnt im Kern. Außerhalb des Kerns brennt
der Wasserstoff als Schale weiter.
Wenn im Kern das Helium verbraucht ist, beginnt im Kern das
Kohlenstoffbrennen. Über dem Kern brennt nun eine
Heliumschale, darüber die Wasserstoffschale.
Nach dem Kohlenstoff brennt Neon, Sauerstoff und schließlich Silizium.
Der Wechsel beim Brennen eines neuen Elementes ist bei diesen Sternen nicht
aufsehenerregend. Sie sind innen nicht entartet.
Das Schalenbrennen endet, wenn im Kern Eisen überhand nimmt.
Eisen kann nicht weiter verbrannt werden.
Siehe auch Bild oben.
Die äußeren Schalen drücken nach unten und haben keinen Gegendruck mehr.
Die Gravitationsenergie der Schalen ist so hoch, dass der Stern als
Typ-IIP-Supernova explodiert und entweder ein
Schwarzes Loch (wenn M > 8 Msonne) oder einen
Neutronenstern hinterlässt.
Blaue Riesen sind selten und kurzlebig. Wegen ihrer äußerst hohen Leuchtkraft
können sie in sehr großen Entfernungen - beispielsweise in nahen Galaxien -
gut aufgefunden werden.
Im Hertzsprung-Russell-Diagramm sind sie überrepräsentiert.
Doppelsterne
In diese Kategorie der Doppelsterne gehören auch Mehrfachsysteme, bei denen
bis zu sieben Sonnen auf komplizierten Bahnen umeinander kreisen.
Heute nimmt man an, dass 60 bis 70% aller Sterne der Milchstraße zu solchen
Mehrfachsternsystemen gehören.
Beispielsweise ist Alpha Centauri ein Dreifachsystem oder
Sirius
ein Doppelsternsystem.
Ursprünglich bezeichnete man alle Sterne, die am Himmel nahe beieinander liegen,
als Doppelsterne. Auch solche Paare, die unterschiedlich weit von uns
weg liegen - der eine Partner beispielsweise 4 Lichtjahre, der andere 500
Lichtjahre - zählte man dazu. Diese sogenannten "optischen Doppelsterne" können
schwerkraftmäßig überhaupt keine Verbindung haben.
Dann gibt es noch die "geometrischen Doppelsterne". Dabei begegnen sich zwei
unabhängige Sterne. Sie lenken durch ihre Schwerkraft einander ab. Aber
aufgrund ihrer hohen Geschwindigkeit entfernen sie sich wieder voneinander.
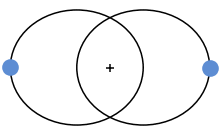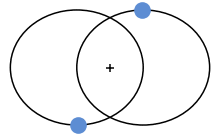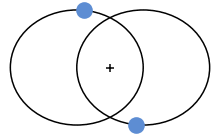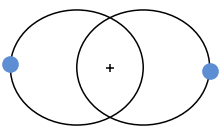 |
Ellipsenbahnen um ein Massenzentrum.
Sie liegen in einer Ebene.
Bildherkunft |
Interessant sind dagegen Sterne, die auf
Ellipsenbahnen dauerhaft umeinander kreisen.
Es kommen alle denkbaren Kombinationen von Sternen vor.
Die Abstände der Partner können sehr unterschiedlich sein - es kann ein
Lichtjahr dazwischen liegen. Die Partner können sich andererseits bis auf die
Roche-Grenze nähern.
Entsprechend unterschiedlich sind die Umlaufszeiten, die Jahrtausende - aber
auch nur Bruchteile eines Tages dauern können.
Die Bahnen sind meist exzentrisch. Bei den beiden Hauptsternen von
Alpha Centauri entspricht die größte Annäherung 11,5AE -
etwa dem Abstand Sonne-Saturn; die größte Entfernung 36,3AE läge weit außerhalb
der Neptunbahn. Proxima Centauri, der dritte Stern, ist 1/4 Lichtjahre
weg und strahlt mit 4,5m selbst dort nur schwach. Er ist nicht zusammen mit den
anderen Sternen entstanden, sondern wurde irgendwann eingefangen.
Wie die zwei Sonnen auf dortigen Planeten erscheinen würden, kann man
nachlesen.
Die weitere Unterscheidung der Doppelsterne richtet sich nach dem Abstand,
unter dem die beiden Sterne am Himmel erscheinen.
Visuelle Doppelsterne erscheinen unter einem Winkel bis hinab zu 0,1".
Einige kann man sogar mit dem Auge trennen, etwa
Mizar und
Alkor.
Sie sind 700" auseinander.
Teleskopische Doppelsterne nennt man jene, die Winkelabstände von 0,1"
bis etwa 100" aufweisen. Um sie trennen zu können, braucht man ein Teleskop -
für 0,1" eines von 1,25m Durchmesser.
Damit sind die visuellen Doppelsterne auf solche in der Nähe der Sonne und auf
solche mit größerem Abstand begrenzt.
Die Bedeckungsveränderlichen oder photometrischen
Doppelsterne muss man nicht optisch trennen können, um mehr über sie zu
erfahren. Aus ihrer Helligkeitskurve kann man Umlaufzeit, Radien, den relativen
Abstand und die Flächenhelligkeit zu berechnen. Aus der Farbe kann man auf die
Temperatur schließen. Der Dopplereffekt liefert uns die
Radialgeschwindigkeit. Damit können die Masse und die Bahnexzentrizität
ermittelt werden.
Im Bild hat der große Stern eine hohe Leuchtkraft, während der
kleine Stern den größeren sogar etwas abdunkelt. Damit wir diese Sterne so
erkennen können, müssen wir von der Seite auf die Bahnebene sehen können.
Wenn die Bahnebene schief steht, bedecken sich die Sterne nicht.
Ein Beispiel für einen Bedeckungsveränderlichen ist
Algol.
Spektroskopische Doppelsterne hat man vor sich, wenn die
beiden Einzelsterne sich einander so eng umkreisen, dass sie im Teleskop nicht
mehr trennbar sind.
Diese Sterne zeigen einen periodischen Dopplereffekt: Wenn sich ein Stern auf
uns zu bewegt, entfernt sich der andere. Im gemeinsamen Spektrum spalten sich
dann die Spektrallinien nach Blau und Rot auf - nach blau, wenn der Stern auf
uns zu kommt - nach rot, wenn er weg geht.
Je stärker die Verschiebung, um so größer ist die radiale Geschwindigkeit.
Aus der Umlaufzeit und den radialen Geschwindigkeiten kann man die Massen
berechnen.
Bei ähnlicher Helligkeit überlagern sich die beiden Farbbänder zu einem
gemischten Spektraltyp. Wenn allerdings die beiden Sterne sehr unterschiedliche
Helligkeiten haben, dann überstrahlt das Spektrum des Hauptsterns das des
Begleiters und die Linienverschiebung ist nur nach einer Seite messbar.
Man kann dann die Massen nicht bestimmen.
 |
| Ellipsenbahnen eines Doppelsterns. |
Für die Berechnung der Bahnen eines Doppelsternsystems muss man zuerst
die Neigung der Ebene mit den beiden Umlaufbahn
herausfinden.
Wenn wir zum Himmel schauen, sehen wir ja immer nur eine Projektion der
Umlaufbahnen. Daraus kann man die eigentlichen Ellipsenbahnen berechnen.
Siehe dazu Bahn von Alpha Centauri B als Beispiel.
Bei visuellen Doppelsternen kann man nicht nur die Projektion auf den Himmel
genau vermessen. Man kann mit dem Doppler-Effekt
auch noch die Radialgeschwindigkeiten der beiden Sterne herausfinden.
Dadurch ist es möglich, den Neigungswinkel der Ellipsenbahnen auszurechnen, und
so auch die exakte Größe der Bahnellipsen.
Durch die Anwendung der Keplerschen Gesetze
kann man nun die Massen der beiden Sterne bestimmen.
Das Bild rechts oben verdeutlicht uns die Bahnen eines Doppelsterns im
Schwerpunktsystems.
Der linke Stern M1 (rot) hat im Bild die doppelte Masse wie Stern M2 (schwarz).
Das Bild zeigt uns den Ort der Sterne an vier Zeitpunkten (t1-t4).
S ist der Schwerpunkt des Systems. Die Bahnellipsen der beiden Sterne liegen so,
dass im Schwerpunkt ein Brennpunkt jeder Ellipse liegt.
a1 und a2 (hellrot) sind deren große
Halbachsen; e1 und e2 (gelb) sind die
Abstände der Mittelpunkte (O1 und O2) zu den
Brennpunkten.
Aus den Halbachsen erhält man das Massenverhältnis:
M1 / M2 = a2 / a1 und die Gesamtmasse:
M1 + M2 = 4 π2 / G ⋅ (a1 + a2) /
T2
(G = 6,67259E-11; T = Umlaufzeit;
M1 = Masse von Stern M1)
Das Bild rechts unten zeigt uns, wie die Bahn des Sternes M2 aussieht,
wenn wir uns vorstellen, auf Stern M1 zu sitzen und uns mit ihm zu bewegen.
Wir haben eine typische Kepler-Ellipse, wobei Stern M1 im Koordinatenursprung
liegt.
Die Bahnneigung kann man nur bei visuellen Doppelsternen herausfinden.
Bei spektroskopischen Doppelsternen hat man ja die Tangentialgeschwindigkeit
nicht. Deshalb kann man bei spektroskopischen Doppelsternen nur das
Massenverhältnis aus den Radialgeschwindigkeiten erkennen:
M1 / M2 = a2 / a1 = v2 / v1.
Die ersten gründlichen Untersuchungen dieser Art gehen auf
Antonia Maury in Harvard zurück.
Die Entwicklung der Doppelsterne
Die schrittweise Entwicklung eines kleineren Doppelstern-System soll hier
beschrieben werden. Es muss sich um ein enges System handeln. Denn nur
bei einem engen System können die Sterne im Laufe der Entwicklung Masse
austauschen.
Ein Stern bläht sich ja am Ende seines Wasserstoffbrennens stark aus.
Er kann auf das mehrere Hundertfache seines Radius anwachsen. Unsere Sonne
wird sich beispielsweise einmal bis zur Erdbahn ausdehnen.
Wenn jedoch die beiden Sterne viel weiter auseinander liegen, so entwickeln sie
sich wie Einzelsterne.
Anders als in dem im Folgenden besprochenen kleinen System läuft die Entwicklung
in einem System mit schwereren Sternen weit dramatischer ab.
Wer mehr dazu wissen will, kann ja
Karttunen... S.291-295 lesen.
 |
| Entwicklung eines Doppelstern-Systems.
|
In den Teilbildern rechts wird davon ausgegangen, dass das Massenverhältnis am
Anfang M1/M2=2 sei. Der linke Stern M1 habe zwei Sonnenmassen, der rechte
Stern M2 nur eine Sonnenmasse. Die Umlaufzeit läge bei 1,4 Tagen.
Das Massenverhältnis ändert sich jedoch im Laufe der Entwicklung.
Die senkrechte gestrichelte Linie zeigt in allen Teilbildern das Massenzentrum.
Die schwarzen Linien in Form einer liegenden 8 zeigen die
Roche-Grenze. Wenn Materie diese Grenze überschreitet,
dann kann sie vom Stern nicht mehr durch die Schwerkraft festgehalten
werden.
- Bild a
-
Wenn sich aus der anfänglichen Staubwolke ein Doppelsternsystem gebildet hat,
so durchläuft jeder dieser beiden Sterne zunächst einmal die
Hauptreihe im
Hertzsprung-Russell-Diagramm.
So lange die beiden Sterne nun in der Hauptreihe sind, ist der Zustand des
Systems stabil. Das kann viele Millionen - wenn nicht Milliarden Jahre - so
bleiben.
- Bild b
-
Die beiden Sterne haben unterschiedliche Massen. Der linke, schwerere
Stern M1 bläht sich zuerst auf. Sein Wasserstoffvorrat im Kern ist zuerst
verbraucht, und der Kern schrumpft. Wegen der steigenden Temperatur dort,
dehnen sich die äußeren Schichten stark aus. Der Stern füllt nun die
Roche-Grenze voll aus, ja überschreitet sie.
- Bild c
-
Nun gibt der zunächst schwerere Stern M1 immer mehr Masse ab. Er verliert immer
mehr von seiner Hülle. Sein Kern erhitzt sich aber immer mehr.
Stern M2 bekommt die Masse. Seine Leuchtkraft steigt stark an.
Er bleibt dabei aber immer noch innerhalb der Roche-Grenze.
Algol ist beispielsweise so ein System.
Nach einigen Millionen Jahren hört der Massenaustausch auf, und Stern M1 wird
zum Weißen Zwerg.
- Bild d
-
Viele Millionen - wenn nicht Milliarden Jahre kreisen der Weiße Zwerg M1 und
der Stern M2 umeinander. Sirius ist beispielsweise so ein System.
- Bild e
-
Irgendwann wird sich am Ende auch Stern M2 aufblähen und Masse an den
Weißen Zwerg M1 abgeben. Auf der Oberfläche von M1 sammelt sich nun Wasserstoff
aus der Hülle von Stern M2. Wenn das Gas etwa 10 Millionen Kelvin erreicht hat,
kann es sich in einer Kernfusion entzünden. Sobald 1E8 Kelvin erreicht sind,
breitet sich die Fusion über den ganzen Stern aus. Da nun die Entartung
aufgehoben ist, wächst der Radius des Weißen Zwergs auf das 1000 bis
10000-fache.
Die Leuchtkraft steigt auch auf das 1000 bis 10000-fache.
Insgesamt werden etwa 1E-4 Sonnenmassen ins All geschleudert. Die Masse auf dem
Weißen Zwerg M1 wächst aber insgesamt weiter an, weil die Fusionsprodukte
zurück bleiben.
Dieser starke Energieausbruch wird als
Nova
bezeichnet - nicht als Supernova.
Nach dem Ausbruch sammelt sich erneut Masse auf dem Weißen Zwerg M1 an, und
der Vorgang kann sich durchaus viele Male wiederholen.
- Bild f
-
Die Masse des Weißen Zwergs wächst weiter an, bis es die
Chandrasekhar-Grenze übersteigt.
Dann fällt der Weiße Zwerg M1 zusammen und explodiert als
Supernova vom Typ Ia. Vom Stern M1 ist danach nichts mehr
übrig.
Diese Supernovae vom Typ Ia geben eine recht genau bekannte Lichtmenge ab.
Sie sind somit ein Hilfsmittel zur
Entfernungsbestimmung weit entfernter
Galaxienhaufen. Leider kommen diese Supernovae nur alle 300 Jahre in einer
Galaxie vor. In Superhaufen mit vielen Tausenden Galaxien kommen sie in
überschaubarer Häufigkeit vor.
Literatur
Allgemein
Wikipedia, auch mit Übernahme von Bildern und
Textbausteinen
aus Artikeln zur Geologie und
Astronomie
Sendungen
alpha-Centauri auf ARD-alpha.
↑
Wolfgang Demtröder: Experimentalphysik 1-4. Heidelberg 1994-1998.
Speziell Astronomie
↑
Karttunen, Kröger, Oja, Poutanen, Donner: Astronomie. Heidelberg 1990.
Layzer, David: Das Universum. Heidelberg 1986.
Otto Struve: Astronomie. Berlin 1962.
Mathias Scholz: Kleines Lehrbuch der Astronomie und Astrophysik 1-15. 2007.
https://www.astronomie.de/kleines-lehrbuch-der-astronomie
Rudolf Wolf: Handbuch der Astronomie. Zürich 1890.
http://ebooks.ethbib.ethz.ch/fulltext/Rara/
Dateien 11121-Band1.pdf bis 11121-Band4.pdf.
Internetauftritt der
ESO.
Internetauftritt
Abenteuer Universum von Halim Paracki.
Strassl: Die erste Bestimmung einer Fixsternentfernung.
In: Die Naturwissenschaften, August 1946, S.65ff.
Bildernachweis
ep0 ↑ :
https://commons.wikimedia.org/wiki/File:Star-sizes.jpg
aus Wikimedia Commons, the free media repository.
Urheber Dave Jarvis.
ep1 ↑ :
https://commons.wikimedia.org/wiki/File:Eratosthenes.svg
aus Wikimedia Commons, the free media repository.
Urheber siehe Wikimedia Commons.
ep2 ↑ :
https://de.wikipedia.org/wiki/Datei:Geometry_of_a_Lunar_Eclipse_DE.svg
aus Wikimedia Commons, the free media repository.
Urheber Sagredo.
ep3 ↑ :
https://commons.wikimedia.org/wiki/File:Kepler_laws_diagram.svg
aus Wikimedia Commons, the free media repository.
Urheber Hankwang.
ep4 ↑ :
https://de.wikipedia.org/wiki/Datei:Venus_parallax_during_the_1769_transit_de.png
aus Wikimedia Commons, the free media repository. Urheber Sch.
ep5 ↑ :
https://commons.wikimedia.org/wiki/File:Fotothek_df_tg_0001484_Geometrie_%5E_Vermessung_%5E_Entfernung_%5E_Winkelinstrument.jpg
aus Wikimedia Commons, the free media repository.
Urheber siehe Wikimedia Commons.
ep6 ↑ :
https://commons.wikimedia.org/wiki/File:ParallaxV2.svg
aus Wikimedia Commons, the free media repository.
Urheber siehe Wikimedia Commons.
ep7 ↑ :
https://commons.wikimedia.org/wiki/File:Leavitt_1912_figures_1%262.png
aus Wikimedia Commons, the free media repository.
Urheber Henrietta Swan Leavitt, William Pickering.
ep10 ↑ :
https://commons.wikimedia.org/wiki/File:Electromagnetic_spectrum_-de_c.svg
aus Wikimedia Commons, the free media repository.
Urheber: Horst Frank.
ep11 ↑ :
https://commons.wikimedia.org/wiki/File:Spectral_luminous_efficacy_1200x1400_wcols_de.png
aus Wikimedia Commons, the free media repository. Urheber Sch.
ep12 ↑ :
https://commons.wikimedia.org/wiki/File:CIE-Normfarbtafel.png
aus Wikimedia Commons, the free media repository.
Urheber Torge Anders.
ep13 ↑ :
https://commons.wikimedia.org/w/index.php?lang=de&title=File%3ASonne_Strahlungsintensitaet.svg
aus Wikimedia Commons, the free media repository. Urheber Degreen.
ep14 ↑ :
https://commons.wikimedia.org/wiki/File:Hg_Niederdruck_Spektrum.png
aus Wikimedia Commons, the free media repository.
Urheber Herbertweidner.
ep15 ↑ :
https://commons.wikimedia.org/wiki/File:Fraunhofer_lines_DE.svg
aus Wikimedia Commons, the free media repository.
Urheber Saperaud.
ep20 ↑ :
https://commons.wikimedia.org/wiki/File:Refraction_on_an_aperture_-_Huygens-Fresnel_principle.svg
aus Wikimedia Commons, the free media repository.
Urheber Arne Nordmann.
ep21 ↑ :
https://commons.wikimedia.org/wiki/File:Interference_of_two_waves.svg
aus Wikimedia Commons, the free media repository.
Urheber siehe Wikimedia Commons.
ep22 ↑ :
https://de.wikibooks.org/wiki/Datei:Double_slit_experiment_(schematic).svg
aus Wikimedia Commons, the free media repository.
Urheber Nobelium. Eigene Änderungen eingefügt.
ep30 ↑ :
https://commons.wikimedia.org/wiki/File:Dopplerfrequenz.gif
aus Wikimedia Commons, the free media repository.
Urheber Charly Whisky.
ep31 ↑ :
https://commons.wikimedia.org/wiki/File:Redshift_blueshift.svg
aus Wikimedia Commons, the free media repository.
Urheber Ales Tosovský.
ep32 ↑ :
https://commons.wikimedia.org/wiki/File:Proper_motion_de.svg
aus Wikimedia Commons, the free media repository.
Urheber CWitte.
ep35 ↑ :
https://commons.wikimedia.org/wiki/File:Redshift.svg
aus Wikimedia Commons, the free media repository.
Urheber siehe Wikimedia Commons.
ep36 ↑ :
https://commons.wikimedia.org/wiki/File:BlackbodySpectrum_loglog_en.svg
aus Wikimedia Commons, the free media repository.
Urheber Prog.
ep37 ↑ :
https://commons.wikimedia.org/wiki/File:Blackbody_peak_wavelength_exitance_vs_temperature.svg
aus Wikimedia Commons, the free media repository.
Urheber CMG Lee.
ep38 ↑ :
https://commons.wikimedia.org/wiki/File:Stellar_Classification_Chart.png
aus Wikimedia Commons, the free media repository.
Urheber Pablo Carlos Budassi.
ep40 ↑ : https://commons.wikimedia.org/wiki/File:Hertzsprung-Russel_StarData_de.jpg
aus Wikimedia Commons, the free media repository.
Urheber Prog.
ep41 ↑ : https://commons.wikimedia.org/wiki/File:Sternentwicklung.png
aus Wikimedia Commons, the free media repository.
Urheber siehe Wikimedia Commons.
ep42 ↑ : https://commons.wikimedia.org/wiki/File:Relative_star_sizes_DE.svg
aus Wikimedia Commons, the free media repository.
Urheber siehe Wikimedia Commons.
ep43 ↑ : https://commons.wikimedia.org/wiki/File:Lebenszyklus_der_Sonne.svg
aus Wikimedia Commons, the free media repository.
Urheber Frank Klemm.
ep44 ↑ : https://de.wikipedia.org/wiki/Datei:Sonnenleben%2B.svg
aus Wikimedia Commons, the free media repository.
Urheber Frank Klemm.
ep45 ↑ : https://commons.wikimedia.org/wiki/File:Layers_of_an_evolved_star.png
aus Wikimedia Commons, the free media repository.
Urheber Pablo Carlos Budassi.
ep50 ↑ : https://commons.wikimedia.org/wiki/File:Binary_system_orbit_q%3D1_e%3D0.5.gif
aus Wikimedia Commons, the free media repository.
Urheber Philip D. Hall.
ep51 ↑ :
https://commons.wikimedia.org/wiki/File:Wiki_Spect_Binaries_v2.gif
aus Wikimedia Commons, the free media repository.
Urheber Primefac.
ep52 ↑ : https://commons.wikimedia.org/wiki/File:Eclipsing_binary_star_animation_2.gif
aus Wikimedia Commons, the free media repository.
Urheber Stanlekub.
Nach oben
Zurück
Drucken
© 2002-2025
Alle Rechte vorbehalten (siehe
Impressum).

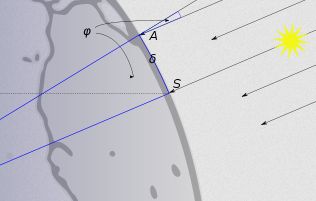
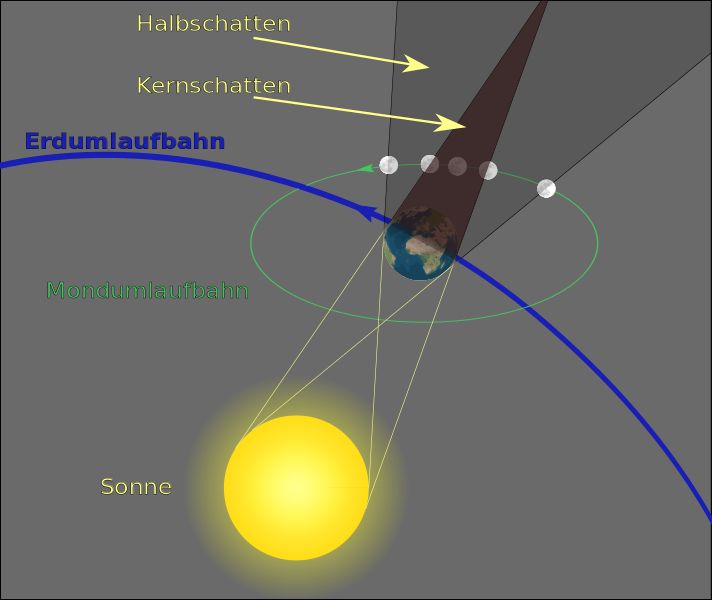
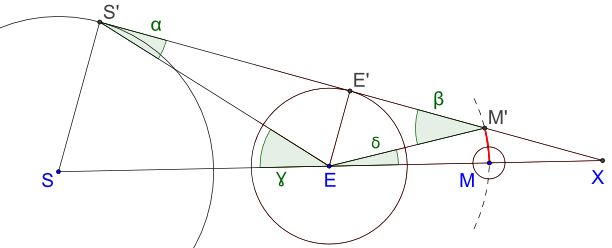
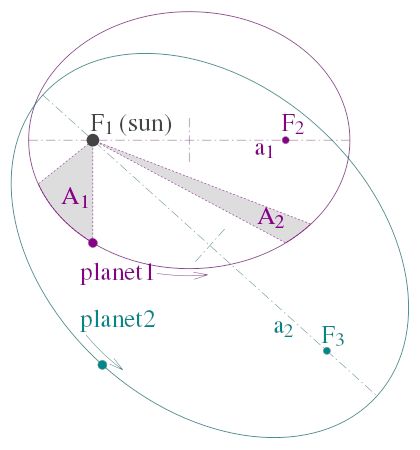
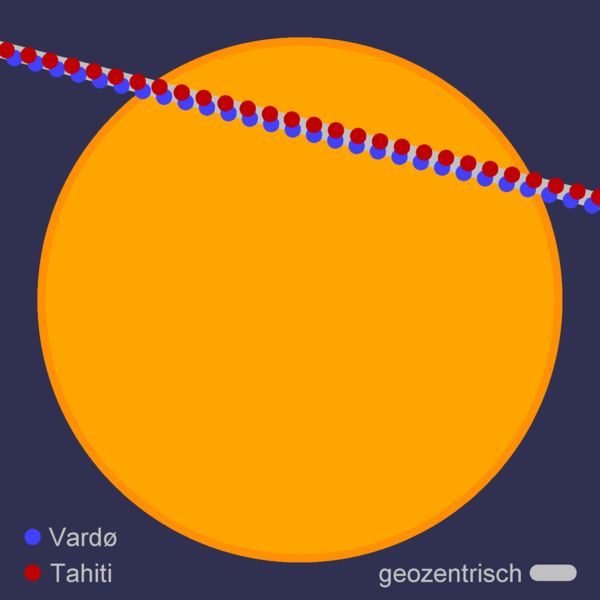


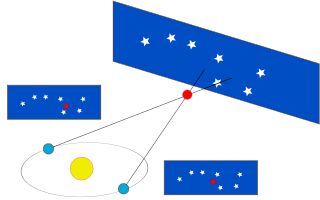
 Bessels Fernrohr, ein Heliometer, hatte vorne - in Richtung zum Stern - eine
geteilte Linse. Die beiden Halblinsen konnte man sehr genau gegeneinander
verschieben. Es ergaben sich so für jeden Stern zwei Brennpunkte, jeweils durch
die obere und die untere Teillinse. Durch Verschieben der einen Teillinse
konnte man nun den einen Brennpunkt des Sterns (A2) mit dem zweiten Brennpunkt
des anderen Sterns (B1) mittels einer Mikrometerschraube übereinander bringen.
Eine Verschiebung einer Teillinse um 1mm entsprach bei Bessels Heliometer einem
Winkelunterschied von etwa 80".
An einer Skala konnte man den Winkelabstand mit einer Genauigkeit von 0,05"
ablesen.
Das Fernrohr kann zum Messen beliebig um seine Längsachse gedreht werden.
Bessels Fernrohr, ein Heliometer, hatte vorne - in Richtung zum Stern - eine
geteilte Linse. Die beiden Halblinsen konnte man sehr genau gegeneinander
verschieben. Es ergaben sich so für jeden Stern zwei Brennpunkte, jeweils durch
die obere und die untere Teillinse. Durch Verschieben der einen Teillinse
konnte man nun den einen Brennpunkt des Sterns (A2) mit dem zweiten Brennpunkt
des anderen Sterns (B1) mittels einer Mikrometerschraube übereinander bringen.
Eine Verschiebung einer Teillinse um 1mm entsprach bei Bessels Heliometer einem
Winkelunterschied von etwa 80".
An einer Skala konnte man den Winkelabstand mit einer Genauigkeit von 0,05"
ablesen.
Das Fernrohr kann zum Messen beliebig um seine Längsachse gedreht werden.